题目内容
已知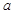 为正实数,
为正实数,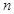 为自然数,抛物线
为自然数,抛物线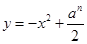 与
与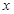 轴正半轴相交于点
轴正半轴相交于点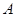 ,设
,设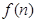 为该抛物线在点
为该抛物线在点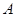 处的切线在
处的切线在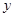 轴上的截距。
轴上的截距。
(1)用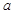 和
和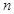 表示
表示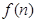 ;
;
(2)求对所有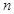 都有
都有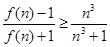 成立的
成立的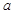 的最小值;
的最小值;
(3)当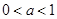 时,比较
时,比较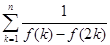 与
与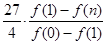 的大小,并说明理由。
的大小,并说明理由。
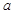 为正实数,
为正实数,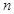 为自然数,抛物线
为自然数,抛物线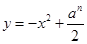 与
与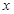 轴正半轴相交于点
轴正半轴相交于点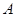 ,设
,设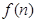 为该抛物线在点
为该抛物线在点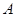 处的切线在
处的切线在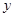 轴上的截距。
轴上的截距。(1)用
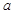 和
和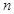 表示
表示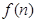 ;
;(2)求对所有
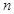 都有
都有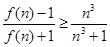 成立的
成立的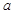 的最小值;
的最小值;(3)当
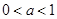 时,比较
时,比较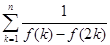 与
与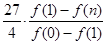 的大小,并说明理由。
的大小,并说明理由。(1)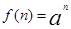 ;
;
(2)a的最小值是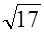 ;
;
(3)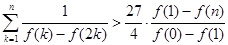 ,证明见解析.
,证明见解析.
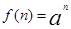 ;
;(2)a的最小值是
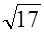 ;
;(3)
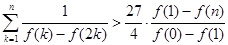 ,证明见解析.
,证明见解析.(1)由已知得,交点A的坐标为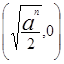 ,对
,对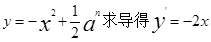 则抛物线在点A处的切线方程为
则抛物线在点A处的切线方程为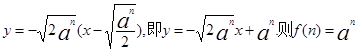
由(1)知f(n)=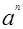 ,则
,则
即知,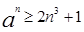 对于所有的n成立,特别地,取n=2时,得到a≥
对于所有的n成立,特别地,取n=2时,得到a≥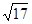
当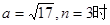 ,
,


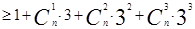
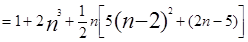 >2n3+1
>2n3+1
当n=0,1,2时,显然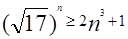
故当a=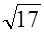 时,
时,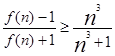 对所有自然数都成立
对所有自然数都成立
所以满足条件的a的最小值是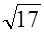 。
。
(3)由(1)知 ,则
,则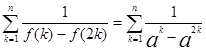 ,
,
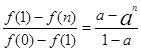
下面证明: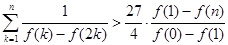
首先证明:当0<x<1时,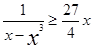
设函数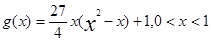
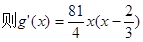
当
故g(x)在区间(0,1)上的最小值g(x)min=g
所以,当0<x<1时,g(x)≥0,即得
由0<a<1知0<ak<1(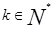 ),因此
),因此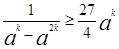 ,从而
,从而
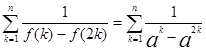
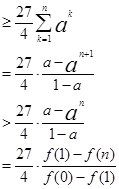
[点评]本小题属于高档题,难度较大,需要考生具备扎实的数学基础和解决数学问题的能力.主要考查了导数的应用、不等式、数列等基础知识;考查了思维能力、运算能力、分析问题与解决问题的能力和创新意识能力;且又深层次的考查了函数、转换与化归、特殊与一般等数学思维方法。
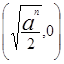 ,对
,对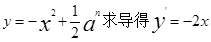 则抛物线在点A处的切线方程为
则抛物线在点A处的切线方程为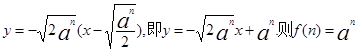
由(1)知f(n)=
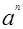 ,则
,则
即知,
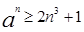 对于所有的n成立,特别地,取n=2时,得到a≥
对于所有的n成立,特别地,取n=2时,得到a≥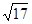
当
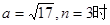 ,
,

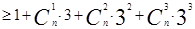
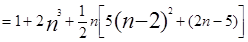 >2n3+1
>2n3+1当n=0,1,2时,显然
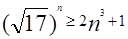
故当a=
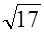 时,
时,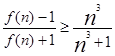 对所有自然数都成立
对所有自然数都成立所以满足条件的a的最小值是
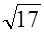 。
。(3)由(1)知
 ,则
,则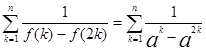 ,
,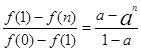
下面证明:
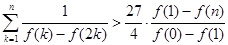
首先证明:当0<x<1时,
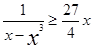
设函数
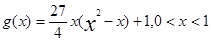
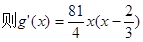
当

故g(x)在区间(0,1)上的最小值g(x)min=g

所以,当0<x<1时,g(x)≥0,即得

由0<a<1知0<ak<1(
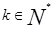 ),因此
),因此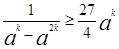 ,从而
,从而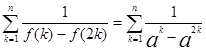
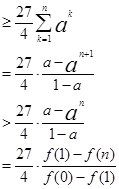
[点评]本小题属于高档题,难度较大,需要考生具备扎实的数学基础和解决数学问题的能力.主要考查了导数的应用、不等式、数列等基础知识;考查了思维能力、运算能力、分析问题与解决问题的能力和创新意识能力;且又深层次的考查了函数、转换与化归、特殊与一般等数学思维方法。

练习册系列答案
相关题目
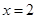 是函数
是函数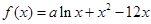 的一个极值点.
的一个极值点.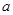 的值;
的值;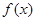 的单调区间.
的单调区间.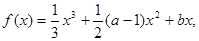 (
(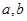 为常数)在
为常数)在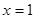 和
和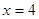 处取得极值,
处取得极值,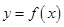 的解析式;
的解析式;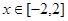 时,
时,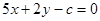 的下方,求实数
的下方,求实数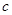 的取值范围.
的取值范围.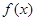 是定义在区间
是定义在区间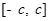 (
(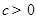 )上的奇函数,令
)上的奇函数,令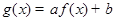 ,并有关于函数
,并有关于函数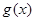 的四个论断:
的四个论断: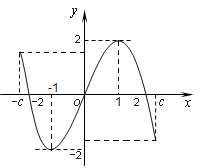
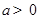 ,对于
,对于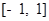 内的任意实数
内的任意实数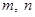 (
(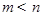 ),
),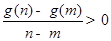 恒成立;
恒成立;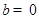 ;
;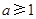 ,
,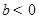 ,则方程
,则方程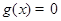 必有3个实数根;
必有3个实数根;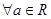 ,
,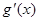 有两个零点;
有两个零点; 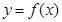 满足:当
满足:当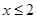 时,
时,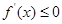 ;当
;当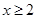 时,
时,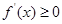 .则下列结论:①
.则下列结论:①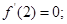 ②
②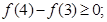 ③
③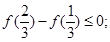 ④
④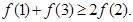 其中成立的个数是( )
其中成立的个数是( )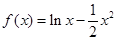 的大致图像是( )
的大致图像是( ) 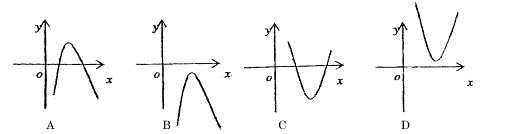
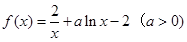 .
.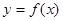 在点
在点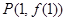 处的切线与直线
处的切线与直线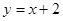 垂直,求函数
垂直,求函数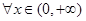 都有
都有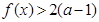 成立,试求
成立,试求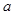 的取值范围;
的取值范围;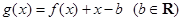 .当
.当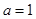 时,函数
时,函数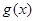 在区间
在区间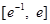 上有两个零点,求实数
上有两个零点,求实数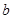 的取值范围.
的取值范围.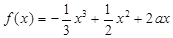 在区间
在区间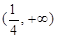 上存在单调递增区间,则的取值范围是
上存在单调递增区间,则的取值范围是