题目内容
18.在数列{an}中,前n项和为Sn,且2Sn=n2+n.(1)求数列{an}的通项公式;
(2)设bn=$\frac{{a}_{n}}{{2}^{n}}$,数列{bn}的前n项和为Tn,求Tn的取值范围.
分析 (1)由${a}_{n}=\left\{\begin{array}{l}{{S}_{1},n=1}\\{{S}_{n}-{S}_{n-1},n≥2}\end{array}\right.$,利用2Sn=n2+n,能求出an.
(2)由bn=$\frac{{a}_{n}}{{2}^{n}}$=$\frac{n}{{2}^{n}}$,利用错位相减法能求出数列{bn}的前n项和为Tn的取值范围.
解答 解:(1)∵数列{an}中,前n项和为Sn,且2Sn=n2+n.
∴n=1时,a1=S1=$\frac{{1}^{2}+1}{2}$=1,
n≥2时,an=Sn-Sn-1=$\frac{{n}^{2}+n}{2}-\frac{(n-1)^{2}+(n-1)}{2}$=n,
n=1时,成立,∴an=n.
(2)∵bn=$\frac{{a}_{n}}{{2}^{n}}$=$\frac{n}{{2}^{n}}$,
∴Tn=$\frac{1}{2}+\frac{2}{{2}^{2}}+\frac{3}{{2}^{3}}+…+\frac{n}{{2}^{n}}$,①
$\frac{1}{2}{T}_{n}$=$\frac{1}{{2}^{2}}+\frac{2}{{2}^{3}}+\frac{3}{{2}^{4}}+…+\frac{n}{{2}^{n+1}}$,②
①-②,得:$\frac{1}{2}{T}_{n}$=$\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+…+\frac{1}{{2}^{n}}-\frac{n}{{2}^{n+1}}$
=$\frac{\frac{1}{2}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$-$\frac{n}{{2}^{n+1}}$
=1-$\frac{1}{{2}^{n}}-\frac{n}{{2}^{n+1}}$,
∴Tn=2-$\frac{2+n}{{2}^{n}}$<2.
∵$\frac{2+n}{{2}^{n}}$随n的增大而减小,∴(Tn)min=T1=2-$\frac{2+1}{2}$=$\frac{1}{2}$,
∴Tn的取值范围是[$\frac{1}{2}$,2).
点评 本题考查数列的通项公式的求法,考查数列的前n项和的求法,是中档题,解题时要认真审题,注意错位相减法的合理运用.

| A. | y=x-2-2 | B. | y=x-2+2 | C. | y=(x-2)-2 | D. | y=(x+2)-2 |
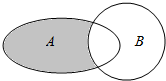 已知全集U=R,函数f(x)=$\left\{\begin{array}{l}{(\frac{1}{3})^{x}-8(x<0)}\\{{x}^{2}+x-1(x≥0)}\end{array}\right.$,集合A={x|x2-2x<3},B={x|f(x)>1},则图中阴影部分所表示的集合为( )
已知全集U=R,函数f(x)=$\left\{\begin{array}{l}{(\frac{1}{3})^{x}-8(x<0)}\\{{x}^{2}+x-1(x≥0)}\end{array}\right.$,集合A={x|x2-2x<3},B={x|f(x)>1},则图中阴影部分所表示的集合为( )| A. | {x|-2<x≤1} | B. | {x|-1<x≤2} | C. | {x|-1<x<1} | D. | {x|-1<x≤1} |
| A. | 不超过19的非负实数 | |
| B. | 方程x2-64=0在实数范围内的解 | |
| C. | $\sqrt{5}$的近似值的全体 | |
| D. | 某育才中学2017级身高超过175cm的同学 |