题目内容
过抛物线y2=2px(p>0)的焦点F作倾斜角为θ的直线交抛物线于A、B两点.设△AOB的面积为S(O为原点).(1)用θ、p表示S;
(2)求S的最小值,若最小值为4时,求此时的抛物线方程.
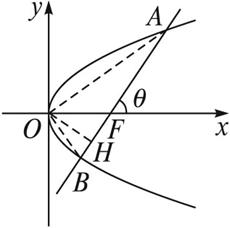
分析:求△AOB的面积有两种途径,一是求顶点到AB的距离OH(如图所示),利用S=![]() |AB|·|OH|;二是将图形进行分割,利用S=S△AOF+S△BOF,把OF看作两三角形的公共底边.
|AB|·|OH|;二是将图形进行分割,利用S=S△AOF+S△BOF,把OF看作两三角形的公共底边.
@@解法一:
(1)设A(x1,y1),B(x2,y2).
若θ=90°时,AB⊥x轴,由抛物线定义,知|AB|=2p,这时|OH|=|OF|=![]() ,
,
∴S△AOB=![]() ·2p·
·2p·![]()
若θ≠90°时,设直线AB方程为y=tanθ(x-![]() ),
),
则|OH|=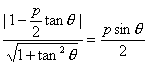 (∵0°<θ<180°).
(∵0°<θ<180°).
从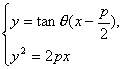 中消去x,得
中消去x,得
y2-(2pcotθ)y-p2=0. ①
∵y1、y2是方程①的两根,
∴y1+y2=2pcotθ,y1y2=-p2.
由弦长公式,得
|AB|=![]() ·|y1-y2|=
·|y1-y2|=![]() ·
·![]()
![]() =(1+cot2θ)·2p
=(1+cot2θ)·2p
![]() ,
,
∴![]() . ②
. ②
当θ=90°时,S=![]() 满足②式,
满足②式,
∴![]()
(2)∵0°<θ<180°,
∴![]() ,当且仅当θ=90°时,等号成立,即Smin=
,当且仅当θ=90°时,等号成立,即Smin=![]() ,表示焦点弦AB变成通径时,△AOB面积最小.
,表示焦点弦AB变成通径时,△AOB面积最小.
令![]() =4,得p=
=4,得p=![]() .
.
∴所求抛物线方程是y2=4![]() x.
x.
解法二:从S=S△AOF+S△BOF

其余同解法一就可得到结论.
绿色通道:
在本题解决的过程中,已证明了焦点弦长公式|AB|=![]() ,由S=
,由S=![]() ,还可推出关系式
,还可推出关系式![]() ,表明对于抛物线y2=2px来讲,S2:|AB|=
,表明对于抛物线y2=2px来讲,S2:|AB|=![]() (定值).
(定值).

练习册系列答案
相关题目
过抛物线y2=2px(p>0)的焦点F的直线l与抛物线在第一象限的交点为A,与抛物线的准线的交点为B,点A在抛物线准线上的射影为C,若
=
,
•
=48,则抛物线的方程为( )
| AF |
| FB |
| BA |
| BC |
| A、y2=4x | ||
| B、y2=8x | ||
| C、y2=16x | ||
D、y2=4
|
过抛物线y2=2px(p>0)的焦点F作直线交抛物线于A、B两点,O为抛物线的顶点.则△ABO是一个( )
| A、等边三角形 | B、直角三角形 | C、不等边锐角三角形 | D、钝角三角形 |