题目内容
 如图,在四棱柱A′B′C′D′-ABCD中,求证:
如图,在四棱柱A′B′C′D′-ABCD中,求证:| AB |
| BC |
| CA′ |
| DD′ |
分析:根据向量的加法法则,易得
+
+
=
+
=
,结合四棱柱的性质得
=
,由此可得原等式成立.
| AB |
| BC |
| CA′ |
| AC |
| CA′ |
| AA′ |
| AA′ |
| DD′ |
解答: 解:如图所示,
解:如图所示,
∵
+
=
,
+
=
,
∴
+
+
=
+
=
,
∵在四棱柱A′B′C′D′-ABCD中,所有侧棱平行且相等
∴向量
=
,
由此可得
+
+
=
,原等式成立
 解:如图所示,
解:如图所示,∵
| AB |
| BC |
| AC |
| AC |
| CA′ |
| AA′ |
∴
| AB |
| BC |
| CA′ |
| AC |
| CA′ |
| AA′ |
∵在四棱柱A′B′C′D′-ABCD中,所有侧棱平行且相等
∴向量
| AA′ |
| DD′ |
由此可得
| AB |
| BC |
| CA′ |
| DD′ |
点评:本题在四棱柱中证明一个向量等式成立,着重考查了平面向量的加法法则和四棱柱的性质等知识,属于基础题.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
 如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是正方形,侧棱与底面垂直,E,F分别是AB1,BC1的中点,则以下结论中不成立的是( )
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是正方形,侧棱与底面垂直,E,F分别是AB1,BC1的中点,则以下结论中不成立的是( ) 中,底面
中,底面 是正方形,侧棱与底面垂直,
是正方形,侧棱与底面垂直, 分别是
分别是 ,
, 的中点,则以下结论中不成立的是( )
的中点,则以下结论中不成立的是( )
 与
与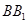 垂直
B.
垂直
B. 垂直
垂直  异面
D.
异面
D. 异面
异面 
 +
+ +
+ =
= .
.