题目内容
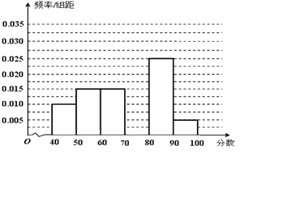
【题目】某校从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60), ...,[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)求成绩落在[70,80)上的频率,并补全这个频率分布直方图;
(Ⅱ) 估计这次考试的及格率(60分及以上为及格)和平均分;
(Ⅲ) 从成绩在[40,50)和[90,100]的学生中任选两人,求他们在同一分数段的概率.
【答案】(Ⅰ)成绩落在[70,80)上的频率是0.3,频率分布直方图见解析;
(Ⅱ)及格率(60分及以上为及格)为: 75﹪,平均分: 71;(Ⅲ) ![]() .
.
【解析】试题分析;(Ⅰ)根据频率分布直方图,用1减去成绩落在其它区间上的频率,即得成绩落在![]() 上的频率,从而补全频率分步直方图.
上的频率,从而补全频率分步直方图.
(Ⅱ) 先根据频率分布直方图,用1减去成绩落在![]() 上的频率,即可得到这次考试的及格率.
上的频率,即可得到这次考试的及格率.
(Ⅲ) 成绩在![]() 的学生人数为
的学生人数为![]() 人,在
人,在![]() 的学生人数为3人
的学生人数为3人
用![]() 表示“从成绩在
表示“从成绩在![]() 和
和![]() 的学生中任选两人,他们的成绩在同一分数段”,
的学生中任选两人,他们的成绩在同一分数段”, ![]() 表示“所选两人成绩落在
表示“所选两人成绩落在![]() 内”,
内”, ![]() 表示“所选两人成绩落在
表示“所选两人成绩落在![]() 内”,则
内”,则![]() 和
和![]() 是互斥事件,由互斥事件的概率可得他们在同一分数段的概率.
是互斥事件,由互斥事件的概率可得他们在同一分数段的概率.
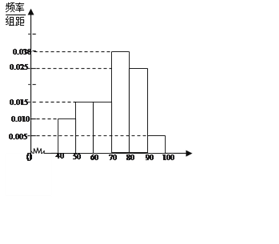
试题解析:(Ⅰ)成绩落在[70,80)上的频率是0.3,频率分布直方图如下图.
 (Ⅱ) 估计这次考试的及格率(60分及以上为及格)
(Ⅱ) 估计这次考试的及格率(60分及以上为及格)
为:1![]() 0.01×10
0.01×10![]() 0.015×10=75﹪
0.015×10=75﹪
平均分:45×0.1+55×0.15+65×0.15+75×0.3
+85×0.25+95×0.05=71
(Ⅲ) 成绩在[40,50)的学生人数为
0.010×10×60=6
在[90,100)的学生人数为
0.005×10×60=3
用A表示“从成绩在[40,50)和[90,100]的学生中任选两人,他们的成绩在同一分数段”, ![]() 表示“所选两人成绩落在[40,50)内”,
表示“所选两人成绩落在[40,50)内”, ![]() 表示“所选两人成绩落在[90,100]内”,则
表示“所选两人成绩落在[90,100]内”,则![]() 和
和![]() 是互斥事件,且
是互斥事件,且
![]() , 从而
, 从而![]() ,
,
因为![]() 中的基本事件个数为15,
中的基本事件个数为15, ![]() 中的基本事件个数为3,全部基本事件总数为36,
中的基本事件个数为3,全部基本事件总数为36,
所以 所求的概率为![]() .
.

 新思维寒假作业系列答案
新思维寒假作业系列答案