题目内容
(本小题满分12分)已知函数 ,
,
(1)对任意实数 ,
, 恒成立,求
恒成立,求 的最小值;
的最小值;
(2)若方程 在区间
在区间 有三个不同的实根,求
有三个不同的实根,求 的取值范围.
的取值范围.
 ,
,
(1)对任意实数
 ,
, 恒成立,求
恒成立,求 的最小值;
的最小值;(2)若方程
 在区间
在区间 有三个不同的实根,求
有三个不同的实根,求 的取值范围.
的取值范围.(1)m的最小值为4
(2) 且
且 或
或
(2)
 且
且 或
或
(1)由已知 对
对 恒成立,
恒成立,
令 ,所以当
,所以当 或
或 时,
时, 取最大值4,所以
取最大值4,所以 ,所以m的最小值为4;…………………………………………………………………………4分
,所以m的最小值为4;…………………………………………………………………………4分
(2)令
则
当 时,
时, 的变化情况如下表
的变化情况如下表
 在
在 上有三个不同实根
上有三个不同实根
 解得
解得 …………………………………………7分
…………………………………………7分
当 时,
时, 的变化情况如下表
的变化情况如下表
 在
在 上有三个不同实根
上有三个不同实根
 解得
解得 且
且 ………………………10分
………………………10分
当 时,
时, ,所以
,所以 在
在 上单调递增,不合题意
上单调递增,不合题意
当 时,
时, 在
在 上单调递减,在
上单调递减,在 上单调递增,所以
上单调递增,所以 在
在 上至多有两个实根,不合题意。
上至多有两个实根,不合题意。
综上 且
且 或
或 ………………………………………
……………………………………… …………………12分
…………………12分
 对
对 恒成立,
恒成立,令
 ,所以当
,所以当 或
或 时,
时, 取最大值4,所以
取最大值4,所以 ,所以m的最小值为4;…………………………………………………………………………4分
,所以m的最小值为4;…………………………………………………………………………4分(2)令

则

当
 时,
时, 的变化情况如下表
的变化情况如下表 | (-1,1) | 1 | (1,a) | a | (a,+∞) |
 | + | 0 | - | 0 | + |
 | 增 | 极大值 | 减 | 极小值 | 增 |
 在
在 上有三个不同实根
上有三个不同实根 解得
解得 …………………………………………7分
…………………………………………7分当
 时,
时, 的变化情况如下表
的变化情况如下表 | (-1,a) | a | (a,1) | 1 | (1,+∞) |
 | + | 0 | - | 0 | + |
 | 增 | 极大值 | 减 | 极小值 | 增 |
 在
在 上有三个不同实根
上有三个不同实根 解得
解得 且
且 ………………………10分
………………………10分当
 时,
时, ,所以
,所以 在
在 上单调递增,不合题意
上单调递增,不合题意当
 时,
时, 在
在 上单调递减,在
上单调递减,在 上单调递增,所以
上单调递增,所以 在
在 上至多有两个实根,不合题意。
上至多有两个实根,不合题意。综上
 且
且 或
或 ………………………………………
……………………………………… …………………12分
…………………12分
练习册系列答案
相关题目
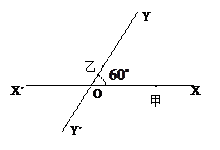
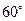 的直路
的直路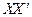 ,
,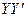 ,交点是
,交点是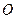 ,甲、乙分别在
,甲、乙分别在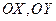 上,起初甲离O点3 km,乙离O点1 km,后甲沿
上,起初甲离O点3 km,乙离O点1 km,后甲沿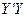 方向用4km/h的速度同时步行. 设t小时后甲在
方向用4km/h的速度同时步行. 设t小时后甲在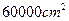 ,四周空白的宽度为
,四周空白的宽度为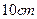 ,栏与栏之间的中缝空白的宽度为
,栏与栏之间的中缝空白的宽度为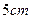 ,怎样确定广告矩形栏目高与宽的尺寸(单位:
,怎样确定广告矩形栏目高与宽的尺寸(单位: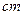 ),能使整个矩形广告面积最小.
),能使整个矩形广告面积最小.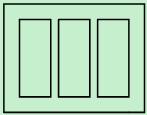
 表示不超过x的最大整数,如
表示不超过x的最大整数,如 ,若
,若 是方程
是方程 的实数根,则( )
的实数根,则( )



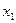 、
、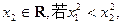 则
则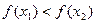 ,现给定函数①
,现给定函数①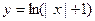 ②
② ③
③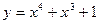
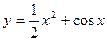
 的零点所在的大致区间是 ( )
的零点所在的大致区间是 ( )



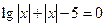 在区间
在区间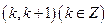 上有零点,则所有满足条件的
上有零点,则所有满足条件的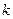 的值的和为 ______.
的值的和为 ______.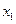 ,
,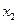 ,……
,……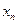 中的最大数为max
中的最大数为max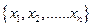 ,最小数为min
,最小数为min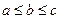 ),定义它的亲倾斜度为
),定义它的亲倾斜度为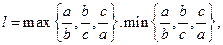
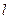 =1”是“
=1”是“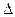 ABC为等边三角形”的
ABC为等边三角形”的