题目内容
若{an}的各项均为正数,前n项和为An,{bn}的前n项和为Bn,且满足Bn=-n(n-1),bn=log2an,求An.
n≥2时,bn=Bn-Bn-1=2(1-n),b1=B1=0符合上式,∴bn=2(1-n)(n∈N*).
又bn=log2an,∴an=
=(
)n-1.∴
=
.
∴{an}是首项为a1=1,公比为q=14的等比数列.
∴An=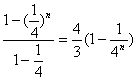
.
练习册系列答案
相关题目
题目内容
若{an}的各项均为正数,前n项和为An,{bn}的前n项和为Bn,且满足Bn=-n(n-1),bn=log2an,求An.
n≥2时,bn=Bn-Bn-1=2(1-n),b1=B1=0符合上式,∴bn=2(1-n)(n∈N*).
又bn=log2an,∴an= =()n-1.∴ =.
∴{an}是首项为a1=1,公比为q=14的等比数列.
∴An=.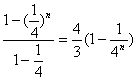
已知等差数列{an}的各项均为正数，观察程序框图；若n=3时，