题目内容
若a＝(cosα，sinα)，b＝(cosβ，sinβ)，且|ka＋b|＝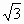
|a－kb|(k＞0，k∈R)．
(1)试用k表示a·b．
(2)求出a·b的最小值，并求出此时a与b夹角θ的大小．
答案：
解析：
解析：
|
解：(1)因为|ka＋b|＝ (2)a·b＝ |
|a－kb|，所以(ka＋b)2＝3(a－kb)2
k2a2＋2ka·b＋b2＝3a2－6ka·b＋3k2b2．又因为a＝(cosα，sinα)，b＝(cosβ，sinβ)，所以|a|＝|b|＝1．所以k2＋2ka·b＋1＝3－6ka·b＋3k2．所以a·b＝
．
(k＋
)≥
，当k＝1时取最小值
．此时cosθ＝
＝
，所以θ＝
．
练习册系列答案
相关题目
)(b＞0)的最大值为
，最小值为－
，求函数y＝－4asin(bx－
)在区间[0，π]上的最大值和最小值．
图像上有两点关于原点对称的不动点，求a、b应满足的条件；
，b＝y2－2z＋
，c＝z2－2x＋
．求证：a，b，c中至少有一个大于0．
}，B＝{x｜|x－1|＜a，a＞0
，若A
B＝A，求a的取值范围．