题目内容
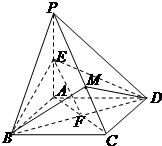
 如图,四棱锥P-ABCD的底面ABCD为菱形,∠ABC=60°,PA⊥底面ABCD,PA=AB=2,E为PA的中点.
如图,四棱锥P-ABCD的底面ABCD为菱形,∠ABC=60°,PA⊥底面ABCD,PA=AB=2,E为PA的中点.(1)求证:PC∥平面EBD;
(2)求三棱锥C-PAD的体积VC-PAD.
考点:棱柱、棱锥、棱台的体积,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(1)设AC、BD相交于点F,连结EF,由已知条件得EF∥PC,由此能证明PC∥平面EBD.
(2)由已知条件得△ACD是边长为2的正三角形,由PA⊥底面ABCD,得PA为三棱锥P-ACD的高,由此能求出三棱锥C-PAD的体积VC-PAD.
(2)由已知条件得△ACD是边长为2的正三角形,由PA⊥底面ABCD,得PA为三棱锥P-ACD的高,由此能求出三棱锥C-PAD的体积VC-PAD.
解答:
 (1)证明:设AC、BD相交于点F,连结EF,
(1)证明:设AC、BD相交于点F,连结EF,
∵底面ABCD为菱形,∴F为AC的中点,
又∵E为PA的中点,∴EF∥PC,…(3分)
又∵EF不包含于平面EBD,PC?平面EBD,
∴PC∥平面EBD. …(6分)
(2)解:因为底面ABCD为菱形,∠ABC=60°,
所以△ACD是边长为2的正三角形,…(8分)
又因为PA⊥底面ABCD,所以PA为三棱锥P-ACD的高,
所以,VC-PAD=
S△ACD•PA=
×
×22×2=
.…(12分)
 (1)证明:设AC、BD相交于点F,连结EF,
(1)证明:设AC、BD相交于点F,连结EF,∵底面ABCD为菱形,∴F为AC的中点,
又∵E为PA的中点,∴EF∥PC,…(3分)
又∵EF不包含于平面EBD,PC?平面EBD,
∴PC∥平面EBD. …(6分)
(2)解:因为底面ABCD为菱形,∠ABC=60°,
所以△ACD是边长为2的正三角形,…(8分)
又因为PA⊥底面ABCD,所以PA为三棱锥P-ACD的高,
所以,VC-PAD=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 4 |
2
| ||
| 3 |
点评:本题考查直线与平面平行的证明,考查三棱锥的体积的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 如图,在直角梯形ABCD中,∠A=∠D=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,SD=
如图,在直角梯形ABCD中,∠A=∠D=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,SD= 如图所示,在五面体ABCDE中,EA=ED=EC=2,且EA,ED,EC两两垂直,AB∥CE,AB=1,F为CD的中点.
如图所示,在五面体ABCDE中,EA=ED=EC=2,且EA,ED,EC两两垂直,AB∥CE,AB=1,F为CD的中点. 如图,A,B为相距2km的两个工厂,以AB的中点O为圆心,半径为2km画圆弧.MN为圆弧上两点,且MA⊥AB,NB⊥AB,在圆弧MN上一点P处建一座学校.学校P受工厂A的噪音影响度与AP的平方成反比,比例系数为1,学校P受工厂B的噪音影响度与BP的平方成反比,比例系数为4.学校P受两工厂的噪音影响度之和为y,且设AP=xkm.
如图,A,B为相距2km的两个工厂,以AB的中点O为圆心,半径为2km画圆弧.MN为圆弧上两点,且MA⊥AB,NB⊥AB,在圆弧MN上一点P处建一座学校.学校P受工厂A的噪音影响度与AP的平方成反比,比例系数为1,学校P受工厂B的噪音影响度与BP的平方成反比,比例系数为4.学校P受两工厂的噪音影响度之和为y,且设AP=xkm.