题目内容
幂函数y=x
①是奇函数但不是偶函数; ②是偶函数但不是奇函数;
③既是奇函数又是偶函数; ④既不是奇函数又不是偶函数.
| 2 | 3 |
②
②
(只需填正确的序号).①是奇函数但不是偶函数; ②是偶函数但不是奇函数;
③既是奇函数又是偶函数; ④既不是奇函数又不是偶函数.
分析:将幂函数y=x
转化为y=
,求出定义域为R,利用奇函数和偶函数的定义,即可判断出正确答案.
| 2 |
| 3 |
| 3 | x2 |
解答:解:幂函数y=x
,变形为y=
,
∴幂函数数y=x
的定义为R,关于原点对称,
∵
=
,
≠-
,
∴幂函数y=x
是偶函数但不是奇函数,
∴正确的是选项②.
故选:②.
| 2 |
| 3 |
| 3 | x2 |
∴幂函数数y=x
| 2 |
| 3 |
∵
| 3 | (-x)2 |
| 3 | x2 |
| 3 | (-x)2 |
| 3 | x2 |
∴幂函数y=x
| 2 |
| 3 |
∴正确的是选项②.
故选:②.
点评:本题考查了幂函数的单调性、奇偶性及其应用.综合考查了幂函数的性质,对于幂函数的问题,关键是正确的画出幂函数的图象,根据幂函数在第一象限的图形,结合幂函数的定义域、奇偶性,即可画出幂函数的图象,应用图象研究幂函数的性质.属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列幂函数在定义域内是单调递增的奇函数的是( )
A、y=x
| ||
| B、y=x4 | ||
| C、y=x3 | ||
D、y=x
|
下面六个幂函数的图象如图所示,试建立函数与图象之间的对应关系.( )
(1)y=x
;(2)y=x
;(3)y=x
;(4)y=x-2;(5)y=x-3;(6)y=x-
.
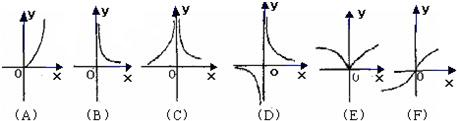
(1)y=x
| 3 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |

| A、(1)?(A),(2)?(F),(3)?(E),(4)?(C),(5)?(D),(6)?(B) |
| B、(1)?(B),(2)?(E),(3)?(C),(4)?(D),(5)?(A),(6)?(F) |
| C、(1)?(A),(2)?(E),(3)?(B),(4)?(D),(5)?(C),(6)?(F) |
| D、(1)?(B),(2)?(F),(3)?(A),(4)?(C),(5)?(D),(6)?(E) |