Question

【题目】如图，A是椭圆的左顶点，点P，Q在椭圆上且均在x轴上方.

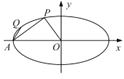
（1）若直线AP与OP垂直，求点P的坐标；

（2）若直线AP，AQ的斜率之积为，求直线PQ的斜率的取值范围.

Answer 1

【答案】(1) (2)

【解析】

（1）设P的坐标，可得向量OP，AP的坐标，由向量垂直的条件：数量积为0，结合P的坐标满足椭圆方程，解方程可得P的坐标；

（2）设出AP，AQ的斜率，以及直线AP，AQ的方程，联立椭圆方程，运用韦达定理，求得P，Q的坐标，和直线PQ的斜率，结合基本不等式可得所求范围．

（1）设，

则，

因为直线AP与OP垂直，

所以，即，

得 ①

又点P在椭圆上，所以②

由①②得或-2（舍去），代入②得，

因为点P在x轴上方，所以.

（2）由于直线AP，AQ的斜率之积为，点P，Q在椭圆上且均在x轴上方.

所以可设直线AP，AQ的斜率分别为，则，

所以直线AP的方程为，

联立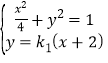得，

设，

则，即，

同理可得，.

所以直线PQ的斜率为

因为，

所以，注意到，点P，Q不重合，所以等号不成立，

所以，

所以直线PQ的斜率的取值范围为