题目内容
某几何体的三视图如图所示，已知其正视图的周长为6，则该 几何体体积的最大值为（ ）分析：由三视图知，判断几何体为圆柱，设其底面的半径为r，高为h，利用周长，列出体积的关系式，通过导数求出最大值即可．
解答：解：由三视图知，该几何体为圆柱，
设其底面的半径为r，高为h，
则4r+2h=6⇒2r+h=3，V=πr2h≤π（
）3=π（当r=h时“=”成立）
或V=πr2h=πr2（3-2r），V'=π[2r（3-2r）-2r2]=6πr（1-r），
令V'=0得r=1，当r∈（0，1）时，V'＞0，
当r∈（1，+∞）时，V'＜0，
故当r=1时，V有最大值，Vmax=π，
故选B．
设其底面的半径为r，高为h，
则4r+2h=6⇒2r+h=3，V=πr2h≤π（
| r+r+h |
| 3 |
或V=πr2h=πr2（3-2r），V'=π[2r（3-2r）-2r2]=6πr（1-r），
令V'=0得r=1，当r∈（0，1）时，V'＞0，
当r∈（1，+∞）时，V'＜0，
故当r=1时，V有最大值，Vmax=π，
故选B．
点评：本题考查三视图与几何体的关系，函数的导数的应用，考查计算能力．
练习册系列答案
相关题目
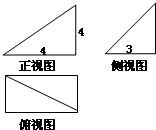
某几何体的三视图如图，它的体积为（ ）
（2012•大连二模）某几何体的三视图如图所示，根据图中尺寸（单位：m），可得该几何体的体积为
（2012•烟台二模）已知某几何体的三视图如图所示，其中，正视图，侧视图均是由三角形与半圆构成，俯视图由圆与内接三角形构成，根据图中的数据可得此几何体的体积为
已知某几何体的三视图如图所示，则几何体的体积为（ ）