题目内容
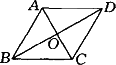
如下图,四边形ABCD是圆柱OQ的轴截面,点P在圆柱OQ的底面圆周上,G是DP的中点,圆柱OQ的底面圆的半径OA=2,侧面积为8 π,∠AOP=120°。
π,∠AOP=120°。
 π,∠AOP=120°。
π,∠AOP=120°。
(1)求证:AG⊥BD;
(2)求二面角P-AG-B的平面角的余弦值。
(2)求二面角P-AG-B的平面角的余弦值。
解:(1)由题意可知
解得
在 中,
中,
∴
又∵G是DP的中点
∴ ①
①
∵ 为圆O的直径
为圆O的直径
∴
由已知知DA⊥底面ABP
∴
∴BP⊥平面DAP
∴ ②
②
∴由①②可知 平面DPB
平面DPB
∴ 。
。
(2)由(1)知: 平面DPB
平面DPB
∴ ,
,
∴ 是二面角
是二面角 的平面角
的平面角
 ,
,

∴
 。
。

解得

在
 中,
中,
∴

又∵G是DP的中点
∴
 ①
①∵
 为圆O的直径
为圆O的直径∴

由已知知DA⊥底面ABP
∴

∴BP⊥平面DAP
∴
 ②
②∴由①②可知
 平面DPB
平面DPB∴
 。
。(2)由(1)知:
 平面DPB
平面DPB∴
 ,
,
∴
 是二面角
是二面角 的平面角
的平面角 ,
,

∴

 。
。
练习册系列答案
相关题目