题目内容
(本题满分12分)成都市为“市中学生知识竞赛”进行选拔性测试,且规定:成绩大于或等于90分的有参赛资格,90分以下(不包括90分)的则被淘汰。若现有500人参加测试,学生成绩的频率分布直方图如下:
(I)求获得参赛资格的人数;
(II)根据频率直方图,估算这500名学生测试的平均成绩;
(III)若知识竞赛分初赛和复赛,在初赛中每人最多有3次选题答题的机会,累计答对2题或答错2题即终止,答对2题者方可参加复赛,已知参赛者甲答对每一个问题的概率都相同,并且相互之间没有影响,已知他连续两次答错的概率为 ,求甲通过初赛的概率.
,求甲通过初赛的概率.
(I) 125;(II)78.48;(III)  .
.
解析试题分析:(I)将频率分布直方图中90~150的小矩形的面积相加,便得获得参赛资格的人数的频率.频率乘以测试总人数500,便得获得参赛资格的人数.
(II)在频率分布直方图中,平均值等于每小组的频率乘以每小组中点的值的和.
(III)已知连续两次答错的概率为 ,由此可得答对每一道题的概率.甲通过初赛包括以下两种情况:连续答对2个或前2题中恰好答对1个且第43个题答对,根据独立事件及互斥事件的概率公式可得甲通过初赛的概率.
,由此可得答对每一道题的概率.甲通过初赛包括以下两种情况:连续答对2个或前2题中恰好答对1个且第43个题答对,根据独立事件及互斥事件的概率公式可得甲通过初赛的概率.
试题解析:(I)获得参赛资格的人数 2分
2分
(II)平均成绩:
 5分
5分
(III)设甲答对每一道题的概率为.P
则

甲通过初赛的概率为: . 12分
. 12分
考点:1、频率分布直方图及样本数据的平均数;2、独立事件与互斥事件的概率.

2013年4月14日,CCTV财经频道报道了某地建筑市场存在违规使用未经淡化海砂的现象.为了研究使用淡化海砂与混凝土耐久性是否达标有关,某大学实验室随机抽取了60个样本,得到了相关数据如下表:
| | 混凝土耐久性达标 | 混凝土耐久性不达标 | 总计 |
| 使用淡化海砂 | 25 |  | 30 |
| 使用未经淡化海砂 | 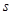 | 15 | 30 |
| 总计 | 40 | 20 | 60 |
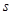 ,
, 的值,利用独立性检验的方法判断,能否在犯错误的概率不超过1%的前提下,认为使用淡化海砂与混凝土耐久性是否达标有关?
的值,利用独立性检验的方法判断,能否在犯错误的概率不超过1%的前提下,认为使用淡化海砂与混凝土耐久性是否达标有关?(Ⅱ)若用分层抽样的方法在使用淡化海砂的样本中抽取了6个,现从这6个样本中任取2个,则取出的2个样本混凝土耐久性都达标的概率是多少?
参考数据:
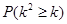 | 0.10 | 0.050 | 0.025 | 0.010 | 0.001 |
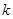 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
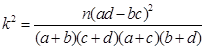
随着工业化的发展,环境污染愈来愈严重.某市环保部门随机抽取60名市民对本市空气质量满意度打分,把数据分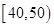 、
、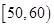 、
、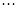 、
、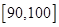 六段后得到如下频率分布表:
六段后得到如下频率分布表:
| 分组 | 频数 | 频率 |
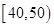 |  | 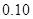 |
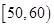 | 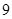 | 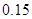 |
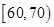 | 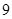 | 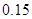 |
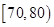 | 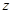 |  |
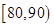 | 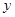 | 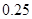 |
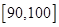 |  | 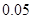 |
| 合计 | 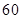 |  |
 、
、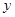 、
、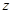 的值;
的值;(2)用分层抽样的方法在分数
 的市民中抽取容量为
的市民中抽取容量为 的样本,将该样本看成一个总体,从中任取
的样本,将该样本看成一个总体,从中任取 人在分数段
人在分数段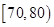 的概率.
的概率. 某种产品的广告费支出 与销售额
与销售额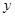 (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据:
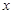 | 2 | 4 | 5 | 6 | 8 |
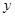 | 30 | 40 | 60 | 50 | 70 |
(2)试预测广告费支出为10万元时,销售额多大?
(3)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过5的概率.
(参考数据:
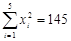


参考公式:线性回归方程系数:
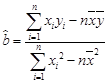 ,
, )
) 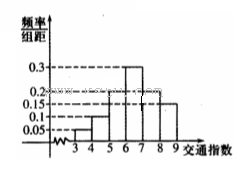
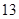 秒与
秒与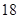 秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组
秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组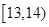 ,第二组
,第二组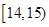 ,…,第五组
,…,第五组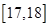 ,下图是按上述分组方法得到的频率分布直方图.
,下图是按上述分组方法得到的频率分布直方图.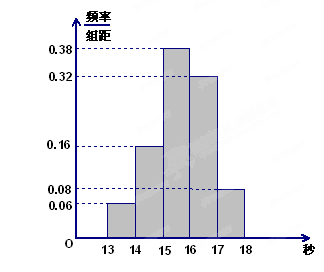

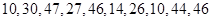

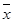 ,将这10株树苗的高度依次输入按程序框图进行的运算,问输出的
,将这10株树苗的高度依次输入按程序框图进行的运算,问输出的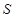 大小为多少?并说明
大小为多少?并说明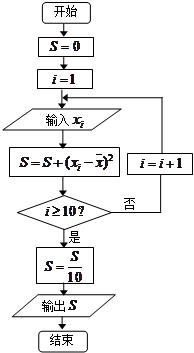
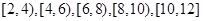 五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在10米到12米之间.
五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在10米到12米之间.
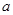 的值及参加“掷实心球”项目测试的人数;
的值及参加“掷实心球”项目测试的人数;
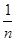 [(x1-
[(x1- )2+(x2-
)2+(x2-