题目内容

已知集合A={a+2,(a+1)2,a2+3a+3},若1∈A,求实数a的值.

解：∵1∈A,∴讨论如下:

(1)若a+2=1,则a=-1.这时有(a+1)2=0,a2+3a+3=(-1)2+3×(-1)+3=1,出现a+2=a2+3a+3,这与集合元素的互异性相矛盾,故a≠-1.

(2)若(a+1)2=1,解得a=0,或a=-2.当a=0时,a+2=2,a2+3a+3=3,这时集合A={1,2,3};当a=-2时,a+2=0,a2+3a+3=1,出现(a+1)2=a2+3a+3,不合题意.

(3)若a2+3a+3=1,则a2+3a+2=0,解得a=-1或a=-2,由(1)知a≠-1.

当a=-2时,a+2=0,(a+1)2=1.这时(a+1)2=a2+3a+3,不合题意.

综上有a=0.

练习册系列答案
相关题目
2、已知集合A={a+2，（a+1）2，a2+3a+3}，B={（a+1）2，5}，若A∩B={1}，则实数a的值为（　　）
1、已知集合A，B，全集∪，给出下列四个命题
（1）若A⊆B，则A∪B=B；
（2）若A∪B=B，则A∩B=B；
（3）若a∈（A∩CUB），则a∈A；
（4）若a∈CU（A∩B），则a∈（A∪B）．
则上述正确命题的个数为（　　）
已知集合A={(x，y)|y=
4-x2
}，集合B={（x，y）|y=x+a}，并且A∩B≠∅，则a的范围是（　　）
已知集合A={x|x2-2ax+4a2-3=0}，集合B={x|x2-x-2=0}，集合C={x|x2+2x-8=0}
（1）是否存在实数a，使A∩B=A∪B？若存在，试求a的值，若不存在，说明理由；
（2）若A∩B≠?，A∩C=∅，求a的值．

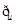已知集合A＝{x|x＜a}，B＝{x|1＜x＜2}，且A∪(B)＝R，则实数a的取值范围是 (　　)

A.a≤2  B.a＜1

C.a≥2  D.a＞2

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网