题目内容
求下列函数的定义域（1）y=tan（2x-
）;
(2)y=
.
解：（1）函数的自变量x应满足：2x-≠kπ+,k∈Z,
即x≠
+
(k∈Z).
所以,函数的定义域为{x|x≠
+
,k∈Z}.
(2)要使函数y=
有意义，
则有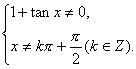
即x≠kπ-
，且x≠kπ+
(k∈Z).
∴函数的定义域为，
{x|x∈R且x≠kπ-
,x≠kπ+
,k∈Z}.
练习册系列答案
一本好题口算题卡系列答案
相关题目
一本好题口算题卡系列答案题目内容
求下列函数的定义域（1）y=tan（2x-）;
(2)y=.
解：（1）函数的自变量x应满足：2x-≠kπ+,k∈Z,
即x≠+(k∈Z).
所以,函数的定义域为{x|x≠+,k∈Z}.
(2)要使函数y=有意义，
则有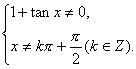
即x≠kπ-，且x≠kπ+(k∈Z).
∴函数的定义域为，
{x|x∈R且x≠kπ-,x≠kπ+,k∈Z}.
一本好题口算题卡系列答案