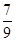题目内容
(1)由“若a,b,c∈R,则(ab)c=a(bc)”类比,若“ ,
, ,
, 为三个向量,则•
为三个向量,则• =
= •”;
•”;(2)在数列an中,a1=0,an+1=2an+2,猜想
 ;
;(3)在平面内“三角形的两边之和大于第三边”类比在空间中“四面体的任意三个面的面积之和大于第四面的面积”;
(4)已知
 ,则a1+a2+…a8=256
,则a1+a2+…a8=256上述四个推理中,得出的结论正确的个数是( )
A.1个
B.2个
C.3个
D.4个
【答案】分析:根据两个向量的数量积的意义可得(1)不正确;构造数列{an+2}构成等比数列,公比为2,首项为a1 +2,求出an+2的解析式即可求得an 的解析式,得(2)正确;由于四面体的任意三个面的面积之和大于第四面的面积是正确的,易得(3)正确;利用二项式定理求得 a1+a2+…a8=-255,故(4)不正确;由此得出结论.
解答:解:由于( •
• )•
)• 表示一个实数乘以
表示一个实数乘以 ,表示一个与
,表示一个与 共线的向量. 而
共线的向量. 而  •(
•( •
• )表示另一个实数乘以
)表示另一个实数乘以 ,表示一个与
,表示一个与 共线的向量,故(1)不正确.
共线的向量,故(1)不正确.
∵an+1=2an+2,∴an+1+2=2(an+2),故数列{an+2}构成等比数列,公比为2,首项为a1 +2=0+2=2,故an+2=2n,即 an =2n-2,故(2)正确.
由于四面体的任意三个面的面积之和大于第四面的面积是正确的,故(3)正确.
由于 ,故 a=
,故 a= 28=256,(2-1)8=256+a1+a2+…a8,∴a1+a2+…a8=-255,故(4)不正确.
28=256,(2-1)8=256+a1+a2+…a8,∴a1+a2+…a8=-255,故(4)不正确.
故选B.
点评:本题主要考查类比推理、二项式定理的应用,求数列的通项公式,两个向量的数量积的意义,属于中档题.
解答:解:由于(
 •
• )•
)• 表示一个实数乘以
表示一个实数乘以 ,表示一个与
,表示一个与 共线的向量. 而
共线的向量. 而  •(
•( •
• )表示另一个实数乘以
)表示另一个实数乘以 ,表示一个与
,表示一个与 共线的向量,故(1)不正确.
共线的向量,故(1)不正确.∵an+1=2an+2,∴an+1+2=2(an+2),故数列{an+2}构成等比数列,公比为2,首项为a1 +2=0+2=2,故an+2=2n,即 an =2n-2,故(2)正确.
由于四面体的任意三个面的面积之和大于第四面的面积是正确的,故(3)正确.
由于
 ,故 a=
,故 a= 28=256,(2-1)8=256+a1+a2+…a8,∴a1+a2+…a8=-255,故(4)不正确.
28=256,(2-1)8=256+a1+a2+…a8,∴a1+a2+…a8=-255,故(4)不正确.故选B.
点评:本题主要考查类比推理、二项式定理的应用,求数列的通项公式,两个向量的数量积的意义,属于中档题.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
 (2011•徐汇区三模)定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”.如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比.已知椭圆
(2011•徐汇区三模)定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”.如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比.已知椭圆 B.
B.
 C.
C.
 D.
D.