题目内容
 如图,椭圆C:
如图,椭圆C:| x2 |
| 16 |
| y2 |
| 4 |
(1)求证:直线DE与直线BP的交点在椭圆C上.
(2)过点B的直线l1,l2与椭圆C分别交于R,S(不同于B点),且它们的斜率k1,k2满足k1•k2=-
| 1 |
| 4 |
分析:(1)确定直线DE与BP的直线方程,可得交点坐标,满足椭圆方程,可得结论;
(2)设出直线方程,求得R,S的坐标,利用R,S关于原点O对称,即可得到结论.
(2)设出直线方程,求得R,S的坐标,利用R,S关于原点O对称,即可得到结论.
解答:证明:(1)由题意,A(4,0),B(0,2),D(0,-2),E(2,0),P(4,1),
则直线DE的方程为y=x-2,直线BP的方程为y=-
x+2
联立方程,可得直线DE与BP的交点坐标为(
,
)
∵椭圆C:
+
=1,∴(
,
)满足方程,
∴直线DE与直线BP的交点在椭圆C上.
(2)直线BR的方程为y=k1x+2
解方程组
,可得
或
∴R的坐标为(-
,
)
∵k1•k2=-
,∴直线BS的斜率k2=-
,∴直线BS的方程为y=-
x+2
解方程组
得
或
∴S的坐标为(
,
)
∴R,S关于原点O对称
∴R,O,S三点共线
∴直线SR过定点,定点的坐标为O(0,0).
则直线DE的方程为y=x-2,直线BP的方程为y=-
| 1 |
| 4 |
联立方程,可得直线DE与BP的交点坐标为(
| 16 |
| 5 |
| 6 |
| 5 |
∵椭圆C:
| x2 |
| 16 |
| y2 |
| 4 |
| 16 |
| 5 |
| 6 |
| 5 |
∴直线DE与直线BP的交点在椭圆C上.
(2)直线BR的方程为y=k1x+2
解方程组
|
|
|
∴R的坐标为(-
| 16k1 |
| 1+4k12 |
| 2-8k12 |
| 1+4k12 |
∵k1•k2=-
| 1 |
| 4 |
| 1 |
| 4k1 |
| 1 |
| 4k1 |
解方程组
|
|
|
∴S的坐标为(
| 16k1 |
| 1+4k12 |
| 8k12-2 |
| 1+4k12 |
∴R,S关于原点O对称
∴R,O,S三点共线
∴直线SR过定点,定点的坐标为O(0,0).
点评:本题考查直线的交点,考查直线与椭圆的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
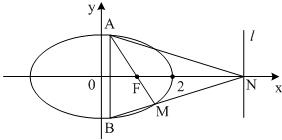 如图,椭圆C:
如图,椭圆C: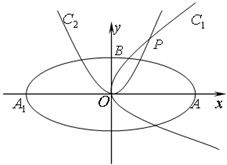 如图,椭圆C:
如图,椭圆C: 如图,椭圆
如图,椭圆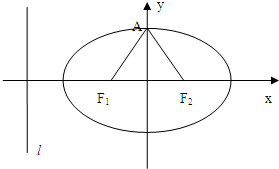 如图,椭圆C:
如图,椭圆C: