题目内容
已知点H(－3，0)，点P在y轴上，点Q在x轴的正半轴上，点M在直线PQ上，且满足
·
＝0，＝－
．
(1)当点P在y轴上移动时，求点M的轨迹G；
(2)过点T(－1，0)作直线l与轨迹G交于A、B两点，若在x轴上存在一点E(x0，0)，使得△ABE是等边三角形，求x0的值．
答案：
解析：
解析：
|
解：(1)设点M的坐标为(x，y)则由 得 由 ∴ ∴M点轨迹G方程： (2)设直线 得 设A(x1，y1)，B(x2，y2)，则x1，x2是方程(1)的两个实数 ∴ AB的垂直平分线为： 令 因为 ∴ ∴ ∴ |
，
，及
·
＝0得
；3分
，由点Q在x轴的正半轴上得
(
)；5分
，其中
代入
(1)；6分
∴AB中点坐标为
，8分
，
；∴点E的坐标为
为正三角形
到直线AB的距离等于
；10分
；12分
．14分
练习册系列答案
新思维寒假作业系列答案
相关题目
已知点H（-3，0），点P在y轴上，点Q在x轴的正半轴上，点M在直线PQ上，且满足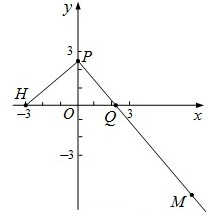
（2009•卢湾区二模）如图，已知点H（-3，0），动点P在y轴上，点Q在x轴上，其横坐标不小于零，点M在直线PQ上，且满足