题目内容
5.已知a1+a2+a3+a4>100,求证:a1,a2,a3,a4中至少有一个数大于25.分析 假设a1,a2,a3,a4均不大于25,则得a1+a2+a3+a4≤25+25+25+25=100,这与已知条件矛盾,故假设不对.
故要证的结论成立.
解答 证明:假设a1,a2,a3,a4均不大于25,
那么,a1+a2+a3+a4≤25+25+25+25=100,这与已知条件矛盾.
所以,a1,a2,a3,a4中,至少有一个数大于25.
点评 本题主要考查用反证法证明数学命题,正确运用反证法的步骤是关键,属于中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
10.高三某学习小组对两个相关变量收集到6组数据如下表:
由最小二乘法得到回归直线方程$\widehat{y}$=0.82x+11.3,发现表中有两个数据模糊不清,则这两个数据的和是89.
| x | 10 | 20 | 30 | 40 | 50 | 60 |
| y | 39 | 28 | m | n | 43 | 41 |
17.已知x,y满足约束条件$\left\{\begin{array}{l}x≥1\\ x+y≤3\\ ay≥x-3\end{array}\right.$,若z=2x+y的最小值为1,则a的值是( )
| A. | 4 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
14.下列命题中的假命题是( )
| A. | ?x∈R,2x>0 | B. | ?a∈(0,1),log${\;}_{\frac{1}{2}}$a>0 | ||
| C. | ?x∈(0,1),x${\;}^{\frac{3}{2}}$<1 | D. | ?α∈(0,$\frac{π}{4}$),sinα+cosα=$\sqrt{2}$ |
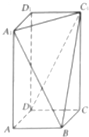 在长方形ABCD-A1B1C1D1中,过A1,C1,B三点的平面截去长方体的一个角后,得到如图所示的几何体,若AB=BC=2,且这个几何体的体积为$\frac{40}{3}$.
在长方形ABCD-A1B1C1D1中,过A1,C1,B三点的平面截去长方体的一个角后,得到如图所示的几何体,若AB=BC=2,且这个几何体的体积为$\frac{40}{3}$.