题目内容
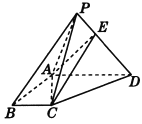
【题目】如图,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 为矩形,平面
为矩形,平面![]() 平面
平面![]() ,
,![]() .
.
(1)求证:![]() 平面
平面![]() .
.
(2)点![]() 在线段
在线段![]() 上运动,设平面
上运动,设平面![]() 与平面
与平面![]() 所成二面角的平面角为
所成二面角的平面角为![]() ,试求
,试求![]() 的取值范围.
的取值范围.
【答案】(1)证明见解析;(2)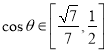 .
.
【解析】
(1)在底面![]() 中证明
中证明![]() 即可证得线面垂直;
即可证得线面垂直;
(2)分别以直线![]() ,
,![]() ,
,![]() 为
为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系,令
轴建立空间直角坐标系,令![]() ,然后写出各点坐标,求出平面
,然后写出各点坐标,求出平面![]() 和平面
和平面![]() 的法向量,由法向量夹角与二面角的关系求得
的法向量,由法向量夹角与二面角的关系求得![]() (为
(为![]() 的函数),由函数知识可得最大值和最小值,即得取值范围.
的函数),由函数知识可得最大值和最小值,即得取值范围.
(1)证明:在梯形![]() 中,∵
中,∵![]() ,
,![]() ,
,![]() ,
,
∴![]() .∴
.∴![]() ,
,
∴![]() ,∴
,∴![]() .
.
∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
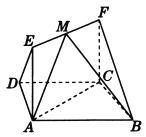
(2)解:分别以直线![]() ,
,![]() ,
,![]() 为
为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系,如图所示,
轴建立空间直角坐标系,如图所示,
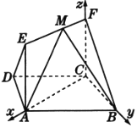
令![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
设![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
由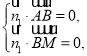 ,得
,得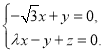
取![]() ,则
,则![]() .
.
∵![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
∴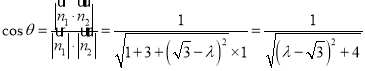 .
.
∵![]() ,
,
∴当![]() 时,
时,![]() 有最小值
有最小值![]() ;
;
当![]() 时,
时,![]() 有最大值
有最大值![]() .
.
∴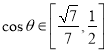 .
.

练习册系列答案
相关题目
【题目】已知![]() 为等差数列,
为等差数列,![]() ,
,![]() ,
,![]() 分别是下表第一、二、三行中的某一个数,且
分别是下表第一、二、三行中的某一个数,且![]() ,
,![]() ,
,![]() 中的任何两个数都不在下表的同一列.
中的任何两个数都不在下表的同一列.
第一列 | 第二列 | 第三列 | |
第一行 | |||
第二行 | 4 | 6 | 9 |
第三行 | 12 | 8 | 7 |
请从①![]() ,②
,②![]() ,③
,③ ![]() 的三个条件中选一个填入上表,使满足以上条件的数列
的三个条件中选一个填入上表,使满足以上条件的数列![]() 存在;并在此存在的数列
存在;并在此存在的数列![]() 中,试解答下列两个问题
中,试解答下列两个问题
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列![]() 满足
满足![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() .
.