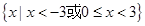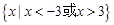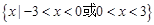题目内容
已知函数 ,
,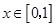
(Ⅰ)求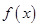 的单调区间和值域;
的单调区间和值域;
(Ⅱ)设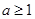 ,函数
,函数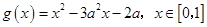 ,若对于任意
,若对于任意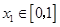 ,总存在
,总存在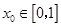 使得
使得 成立,求
成立,求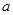 的取值范围。
的取值范围。
 ,
,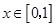
(Ⅰ)求
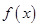 的单调区间和值域;
的单调区间和值域;(Ⅱ)设
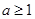 ,函数
,函数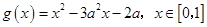 ,若对于任意
,若对于任意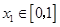 ,总存在
,总存在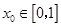 使得
使得 成立,求
成立,求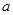 的取值范围。
的取值范围。(Ⅰ) 的单调递减区间为
的单调递减区间为 ,
, 的单调递增区间为
的单调递增区间为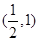 ,
,
 的值域为[-4,-3]
的值域为[-4,-3]
(Ⅱ)
 的单调递减区间为
的单调递减区间为 ,
, 的单调递增区间为
的单调递增区间为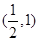 ,
, 的值域为[-4,-3]
的值域为[-4,-3](Ⅱ)

【错解分析】利用导数求函数的单调区间仍然要树立起定义域优先的意识,同时要培养自已的求导及解不
等式的运算能力。第(Ⅱ)问要注意将问题进行等价转化即转化为函数
 在区间
在区间 上的值域
上的值域是函数
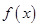 的值域的子集,从而转化为求解函数
的值域的子集,从而转化为求解函数 在区间
在区间 上的值域。
上的值域。【正解】(Ⅰ)
 ,令
,令 解得
解得 或
或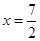 ,在
,在 ,
,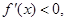 所以
所以 为单调递减函数;在
为单调递减函数;在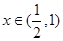 ,
, 所以
所以 为单调递增函数;又
为单调递增函数;又 ,即
,即 的值域为[-4,-3],所以
的值域为[-4,-3],所以 的单调递减区间为
的单调递减区间为 ,
, 的单调递增区间为
的单调递增区间为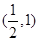 ,
, 的值域为[-4,-3].( 单调区间为闭区间也可以).
的值域为[-4,-3].( 单调区间为闭区间也可以).(Ⅱ)∵
 ,又
,又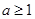 ,当
,当 时,
时,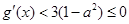 ,
,因此,当
 时,
时, 为减函数,从而当
为减函数,从而当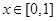 时,有
时,有 .
.又
 ,即当
,即当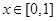 时,有
时,有 ,
,任给
 ,有
,有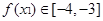 ,存在
,存在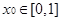 使得
使得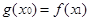 ,
,则
 又
又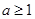 ,所以
,所以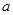 的取值范围是
的取值范围是 。
。【点评】高考对导数的考查定位于作为解决初等数学问题的工具出现,侧重于考查导数在函数与解析几何中的应用,主要有以下几个方面:①运用导数的有关知识,研究函数最值问题,一直是高考长考不衰的热点内容.另一方面,从数学角度反映实际问题,建立数学模型,转化为函数的最大值与最小值问题,再利用函数的导数,顺利地解决函数的最大值与最小值问题,从而进一步地解决实际问题.用导数研究函数的性质比用初等方法研究要方便得多,单调区间的求解过程,已知
 (1)分析
(1)分析  的定义域; (2)求导数
的定义域; (2)求导数  (3)解不等式
(3)解不等式 ,解集在定义域内的部分为增区间(4)解不等式
,解集在定义域内的部分为增区间(4)解不等式 ,解集在定义域内的部分为减区间,对于函数单调区间的合并:函数单调区间的合并主要依据是函数
,解集在定义域内的部分为减区间,对于函数单调区间的合并:函数单调区间的合并主要依据是函数 在
在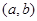 单调递增,在
单调递增,在 单调递增,又知函数在
单调递增,又知函数在 处连续,因此
处连续,因此 在
在 单调递增。同理减区间的合并也是如此,即相邻区间的单调性相同,且在公共点处函数连续,则二区间就可以合并为以个区间。
单调递增。同理减区间的合并也是如此,即相邻区间的单调性相同,且在公共点处函数连续,则二区间就可以合并为以个区间。
练习册系列答案
相关题目
 .
. 的一系列对应值如下表:
的一系列对应值如下表:





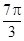
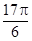



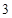
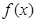 的解析式;
的解析式;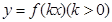 周期为
周期为 ,求
,求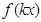 在区间
在区间 上的最大、最小值及对应的
上的最大、最小值及对应的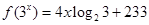 ,则
,则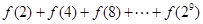 的值等于 .
的值等于 .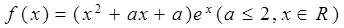
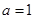 ,求函数
,求函数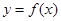 在点(0,
在点(0,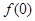 )处的切线方程;
)处的切线方程;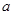 ,使得
,使得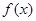 的极大值为3.若存在,求出
的极大值为3.若存在,求出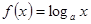 ,在
,在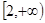 上恒有
上恒有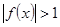 ,则实数
,则实数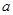 的范围是( )
的范围是( )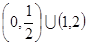
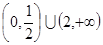


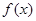 满足条件:
满足条件: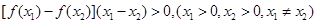 ;
;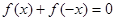
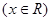 ; ③
; ③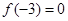 .
.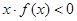 的解集是( )
的解集是( )