题目内容
7．已知四棱锥P-ABCD的顶点都在球O上，底面ABCD是矩形，平面PAD⊥平面ABCD，△PAD为正三角形，AB=4，AD=2，则球O的表面积为（ ）| A． | $\frac{32π}{3}$ | B． | $\frac{64π}{3}$ | C． | 32π | D． | 64π |
分析 求出△PAD所在圆的半径，利用勾股定理求出球O的半径R，即可求出球O的表面积．
解答 解：令△PAD所在圆的圆心为O1，△PAD为正三角形，AD=2，则圆O1的半径r=$\frac{2\sqrt{3}}{3}$，
因为平面PAD⊥底面ABCD，AB=4，
所以OO1=$\frac{1}{2}$AB=2，
所以球O的半径R=$\sqrt{4+（\frac{2\sqrt{3}}{3}）^{2}}$=$\frac{4\sqrt{3}}{3}$，
所以球O的表面积=4πR2=$\frac{64π}{3}$．
故选：B．
点评 本题考查球O的表面积，考查学生的计算能力，比较基础．
练习册系列答案
阅读快车系列答案
相关题目
13．
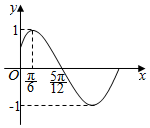已知函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则$\sum_{n=1}^{2016}$f（$\frac{nπ}{6}$）=（ ）
已知函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则$\sum_{n=1}^{2016}$f（$\frac{nπ}{6}$）=（ ）| A． | -1 | B． | $\frac{1}{2}$ | C． | 1 | D． | 0 |
12．在某校冬季长跑活动中，学校要给获得一二等奖的学生购买奖品，要求花费总额不得超过200元，已知一等奖和二等奖奖品的单价分别为20元、10元，一等奖人数与二等奖人数的比值不得高于$\frac{1}{3}$，且获得一等奖的人数不能少于2人，那么下列说法中错误的是（ ）
| A． | 最多可以购买4份一等奖奖品 | B． | 最多可以购买16份二等奖奖品 | ||
| C． | 购买奖品至少要花费100元 | D． | 共有20种不同的购买奖品方案 |
19．下列函数中与f（x）=2x+2-x具有相同的奇偶性的是（ ）
| A． | y=sinx | B． | y=x2+x+1 | C． | y=|x| | D． | y=|lgx| |