题目内容
已知向量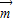 =(-2sin(π-x),cosx),
=(-2sin(π-x),cosx),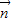 =(
=(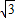 cosx,2sin(
cosx,2sin(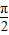 -x)),函数f(x)=1-
-x)),函数f(x)=1-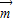 •
•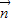 .
.(1)求函数f(x)的解析式;
(2)求f(x)的周期及单调递增区间.
【答案】分析:(1)直接利用向量的数量积,通过二倍角公式与两角差的正弦函数,化简函数我一个角的一个三角函数的形式,即可求函数f(x)的解析式;
(2)利用正弦函数的单调增区间,构造关于相位角的不等式,解不等式可求出函数的单调增区间到.
解答:解:(1)∵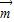 •
•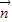 =
=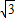 2sin(π-x)
2sin(π-x)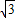 cosx+2cosxsin(
cosx+2cosxsin(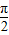 -x)
-x)
=-2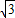 sinxcosx+2cos2x=-
sinxcosx+2cos2x=-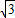 sin2x+cos2x+1 2分
sin2x+cos2x+1 2分
∴f(x)=1-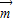 •
•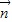 =
=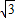 sin2x-cos2x,…(3分)
sin2x-cos2x,…(3分)
∴f(x)=2sin(2x-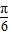 ).…(4分)
).…(4分)
(2)由(1)知f(x)的周期为π由-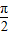 +2kπ≤2x-
+2kπ≤2x-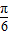 ≤
≤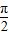 +2kπ (k∈Z),
+2kπ (k∈Z),
解得-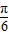 +kπ≤x≤
+kπ≤x≤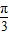 +kπ (k∈Z)…(6分)
+kπ (k∈Z)…(6分)
∴f(x)的单调递增区间为[-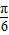 +kπ,
+kπ,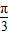 +kπ](k∈Z)…(12分)
+kπ](k∈Z)…(12分)
点评:本题借助向量的数量积的化简,求解函数的解析式,考查三角函数的基本性质,函数的图象的变换.
(2)利用正弦函数的单调增区间,构造关于相位角的不等式,解不等式可求出函数的单调增区间到.
解答:解:(1)∵
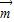 •
•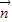 =
=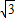 2sin(π-x)
2sin(π-x)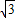 cosx+2cosxsin(
cosx+2cosxsin(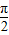 -x)
-x)=-2
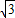 sinxcosx+2cos2x=-
sinxcosx+2cos2x=-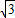 sin2x+cos2x+1 2分
sin2x+cos2x+1 2分∴f(x)=1-
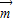 •
•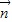 =
=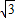 sin2x-cos2x,…(3分)
sin2x-cos2x,…(3分)∴f(x)=2sin(2x-
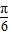 ).…(4分)
).…(4分)(2)由(1)知f(x)的周期为π由-
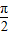 +2kπ≤2x-
+2kπ≤2x-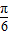 ≤
≤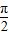 +2kπ (k∈Z),
+2kπ (k∈Z),解得-
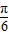 +kπ≤x≤
+kπ≤x≤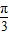 +kπ (k∈Z)…(6分)
+kπ (k∈Z)…(6分)∴f(x)的单调递增区间为[-
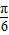 +kπ,
+kπ,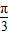 +kπ](k∈Z)…(12分)
+kπ](k∈Z)…(12分)点评:本题借助向量的数量积的化简,求解函数的解析式,考查三角函数的基本性质,函数的图象的变换.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目