题目内容
18.已知函数f(x)=$\left\{\begin{array}{l}{(a-1)x+4,x≤7}\\{{a}^{x-6},x>7}\end{array}\right.$;(1)当a=$\frac{1}{2}$时,f(x)的值域为(0,+∞),
(2)若f(x)是(-∞,+∞)上的减函数,则实数a的取值范围是[$\frac{1}{2},1$).
分析 (1)a=$\frac{1}{2}$时,得到f(x)=$\left\{\begin{array}{l}{-\frac{1}{2}x+4}&{x≤7}\\{(\frac{1}{2})^{x-6}}&{x>7}\end{array}\right.$,根据f(x)在(-∞,7],和(7,+∞)上的单调性即可得出f(x)在每段上的范围,求并集即可得出该函数的值域;
(2)根据一次函数、指数函数的单调性及减函数的定义即可得到$\left\{\begin{array}{l}{a-1<0}\\{0<a<1}\\{(a-1)•7+4≥{a}^{7-6}}\end{array}\right.$,解该不等式组即可得出实数a的取值范围.
解答 解:(1)$a=\frac{1}{2}$时,$f(x)=\left\{\begin{array}{l}{-\frac{1}{2}x+4}&{x≤7}\\{(\frac{1}{2})^{x-6}}&{x>7}\end{array}\right.$;
①x≤7时,f(x)=$-\frac{1}{2}x+4≥\frac{1}{2}$;
②x>7时,f(x)=$(\frac{1}{2})^{x-6}$;
x-6>1;
∴$0<(\frac{1}{2})^{x-6}<\frac{1}{2}$;
即$0<f(x)<\frac{1}{2}$;
∴f(x)的值域为(0,+∞);
(2)f(x)在(-∞,+∞)上单调递减;
∴$\left\{\begin{array}{l}{a-1<0}\\{0<a<1}\\{(a-1)•7+4≥{a}^{7-6}}\end{array}\right.$;
解得$\frac{1}{2}≤a<1$;
∴实数a的取值范围为$[\frac{1}{2},1)$.
故答案为:(1)(0,+∞),(2)[$\frac{1}{2}$,1).
点评 考查一次函数、指数函数的单调性,根据函数单调性求值域,减函数的定义,以及分段函数的单调性的判断.

| A. | 5 | B. | 9 | C. | 7 | D. | 8 |
| A. | (-∞,1) | B. | (-1,1) | C. | (3,+∞) | D. | (1,3) |
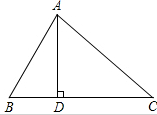 如图,在△ABC中,AD⊥BC,$\frac{\overrightarrow{AB}}{|\overrightarrow{AB|}}$•$\frac{\overrightarrow{AC}}{|\overrightarrow{AC|}}$=$\frac{\sqrt{2}}{2}$,BD=4,CD=6.
如图,在△ABC中,AD⊥BC,$\frac{\overrightarrow{AB}}{|\overrightarrow{AB|}}$•$\frac{\overrightarrow{AC}}{|\overrightarrow{AC|}}$=$\frac{\sqrt{2}}{2}$,BD=4,CD=6.