题目内容

已知0＜a＜b＜1,比较logab,logba,的大小.

 

解法一：（综合法）∵0＜a＜b＜1,

∴＞＞1.

∵y=logax和y=logbx都是区间(0,+∞)上的减函数，和都是区间(0,+∞)上的增函数，

∴logab＞loga1=0,logba＞logb1=0,

,.

∵logab＜logaa=1=logbb＜logba,

,

∴＜logab＜logba.

解法二：（数形结合法）由对数函数的性质及0＜a＜b＜1,可以得到函数y=logax,y=logbx, ,

图象的大致位置如图所示.

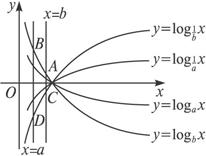
    作直线x=a和x=b可以得到logab,logba, ,的对应点A，B，C，D.

由此可以判断它们的大小关系为：logab＜logba.


练习册系列答案
相关题目
已知0＜a＜b＜1，则ab，logba，log
1
a
b的关系是（　　）
A、log
1
a
b＜ab＜logba
B、log
1
a
b＜logba＜ab
C、logba＜log
1
a
b＜ab
D、ab＜log
1
a
b＜logba
已知0＜a＜b＜1，设aa，ab，ba，bb中的最大值是M，最小值是m，则M=
ba
ba
，m=
ab
ab
．
已知0＜a＜b＜1＜c，m=lo
g
 
a
c，n=lo
g
 
b
c，r=ac，则m，n，r的大小关系是（　　）
已知0＜a＜b＜1，则a+b，a2+b2，2ab从小到大的顺序依次是
2ab＜a2+b2＜a+b
2ab＜a2+b2＜a+b
．
已知0＜a＜b＜1，则（　　）
A、
1
b
＞
1
a
B、（
1
2
）a＜（
1
2
）b
C、（lga）2＜（lgb）2
D、
1
lga
＞
1
lgb

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网