题目内容
以椭圆
+
=1的中心为顶点，以椭圆的左准线为准线的抛物线与椭圆右准线交于A、B两点，则|AB|的值为 ．
【答案】分析：先根据椭圆的方程求得其右准线和左准线即抛物线的准线方程，进而根抛物线的性质求得抛物线的方程，进而把抛物线方程与右准线方程联立求得A，B的坐标，进而根据两点间的距离公式求得答案．
解答：解：依题意可知抛物线的中心为（0，0），左准线为x=-
，
∴抛物线方程为y2=
x．
又∵椭圆右准线方程为x=
，
联立解得A（
，
）、B（
，-
）．
∴|AB|=|
+
|=
．
故答案为：
点评：本题主要考查了抛物线和椭圆的简单性质，圆锥曲线的共同特征．考查了考生综合分析问题和解决问题的能力．
解答：解：依题意可知抛物线的中心为（0，0），左准线为x=-
，∴抛物线方程为y2=
x．又∵椭圆右准线方程为x=
，联立解得A（
，）、B（，-）．∴|AB|=|
+|=．故答案为：
点评：本题主要考查了抛物线和椭圆的简单性质，圆锥曲线的共同特征．考查了考生综合分析问题和解决问题的能力．
练习册系列答案
相关题目
+
=1的中心为顶点，以椭圆的左准线为准线的抛物线与椭圆右准线交于A、B两点，则|AB|的值为________________.
+
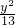=1的焦点为焦点，以抛物线y2=-2
x的准线为右准线．
•
=0？
在椭圆C上，抛物线E以椭圆C的中心为顶点，F2为焦点．