题目内容
(12分)正方形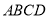 所在平面与平面四边形
所在平面与平面四边形 所在平面互相垂直,△
所在平面互相垂直,△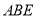 是等腰直角三角形,
是等腰直角三角形,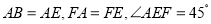
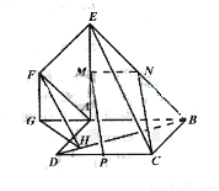
(1)求证: ;
;
(2)设线段 的中点为
的中点为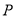 ,在直线
,在直线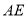 上是否存在一点
上是否存在一点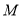 ,使得
,使得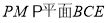 ?若存在,请指出点
?若存在,请指出点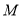 的位置,并证明你的结论;若不存在,请说明理由;
的位置,并证明你的结论;若不存在,请说明理由;
(1)详见解析;(2)存在点 为
为 的中点,使得
的中点,使得 .
.
【解析】
试题分析:(1)要想证明 ⊥平面
⊥平面 ,只需证
,只需证 ⊥
⊥ 、
、 ⊥
⊥ ,其中
,其中 ⊥
⊥ ,可由平面
,可由平面 ⊥平面
⊥平面 ,
, ⊥交线
⊥交线 ,即
,即 ⊥平面
⊥平面 得到.而
得到.而 ⊥
⊥ 可由
可由 ,
, 得到;(2)存在点
得到;(2)存在点 ,要使
,要使 ,则需在平面
,则需在平面 上找到一条
上找到一条 的平行线,因为线段
的平行线,因为线段 的中点为
的中点为 ,所以
,所以 ,由此可以想到取点
,由此可以想到取点 为
为 的中点,点
的中点,点 为
为 的中点,连接
的中点,连接 ,即可得到四边形
,即可得到四边形 为平行四边形,从而使问题得到解决.
为平行四边形,从而使问题得到解决.
试题解析:(1)因为平面 ⊥平面
⊥平面 ,
,
 平面
平面 ,平面
,平面
 平面
平面
 ,又
,又 ⊥
⊥ ,所以
,所以 ⊥平面
⊥平面 ,所以
,所以 ⊥
⊥ .
.
因为 为等腰直角三角形,
为等腰直角三角形, ,所以
,所以 ,又因为
,又因为 ,所以
,所以 ,即
,即 ⊥
⊥ .
.
又


 ,所以
,所以 ⊥平面
⊥平面 .
.
(2)存在点 ,当
,当 为线段
为线段 的中点时,
的中点时, ∥平面
∥平面 ,取
,取 的中点
的中点 ,连接
,连接 ,则
,则 ∥
∥ ∥
∥ ,所以四边形
,所以四边形 为平行四边形,所以
为平行四边形,所以 ∥
∥ ,因为
,因为 在平面
在平面 内,
内, 不在平面
不在平面 内,所以
内,所以 ∥平面
∥平面 .
.
考点:(1)线面垂直的判定;(2)存在性问题中,特殊点的选择以及线面平行的判定.

练习册系列答案
相关题目
已知某地区中小学生人数和近视情况如下表所示:
年级 | 人数 | 近视率 |
小学 | 3500 | 10% |
初中 | 4500 | 30% |
高中 | 2000 | 50% |
为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,
则:(Ⅰ)样本容量为___________;(Ⅱ)抽取的高中生中,近视人数为___________.
 画出输入自变量
画出输入自变量 的值求函数值y的程序框图
的值求函数值y的程序框图 ,
, 为
为 中点,则
中点,则 、
、 的概率是( )
的概率是( ) B.
B. C.
C. D.
D.
 ,
, ,若
,若 ,求实数
,求实数 的取值范围.
的取值范围. ,则
,则 =
=