题目内容
 在等腰梯形ABCD中,AB=3,AD=BC=2,CD=1,E为AB上的点且AE=1,将△AED沿DE折起到A1ED的位置,使得二面角A1-CD-E的平面角为30°.
在等腰梯形ABCD中,AB=3,AD=BC=2,CD=1,E为AB上的点且AE=1,将△AED沿DE折起到A1ED的位置,使得二面角A1-CD-E的平面角为30°.(1)求证:DE⊥A1B;
(2)求二面角B-A1C-D的余弦值.
分析:(1)由题设条件与图,可先证DE⊥面A1EB再有线面垂直证DE⊥A1B;
(2)如图建立空间直角坐标系,设E1A与X轴所的角为θ,给出各点的坐标,设出两个半平面的法向量,由公式求出两个半平面的法向量,再由公式求出二面角B-A1C-D的余弦值
(2)如图建立空间直角坐标系,设E1A与X轴所的角为θ,给出各点的坐标,设出两个半平面的法向量,由公式求出两个半平面的法向量,再由公式求出二面角B-A1C-D的余弦值
解答: 解:(1)证明:如左图,因为在等腰梯形ABCD中,AB=3,CD=1,AE=1,所以DE⊥AB,∴如右图中,DE⊥A1E,DE⊥BE,∴DE⊥面A1EB,故DE⊥A1B,
解:(1)证明:如左图,因为在等腰梯形ABCD中,AB=3,CD=1,AE=1,所以DE⊥AB,∴如右图中,DE⊥A1E,DE⊥BE,∴DE⊥面A1EB,故DE⊥A1B,
(2)如图建立空间直角坐标系,设E1A与X轴所的角为θ,则A1(cosθ,-sinθ,0),B(0,2,0),C(0,1,
)D(0,0,
),设平面A1CD的法向量为
=(x,y,z),平面BCDE的法向量为
=(1,0,0),则
令z=1,则
=(
,0,1),∵cos<
,
>=
,∴
=
,解得cosθ=1,即θ=0
此时,点A1在X轴上,A1(1,0,0),
=(-1,2,0),
=(
,0,1),设平面A1BC的法向量为
=(x,y,z),则
,令y=1,得
=(2,1,
),故cos<
,
>=
=
结合图形,可得二面角B-A1C-D为钝角,故二面角的余弦值为-
 解:(1)证明:如左图,因为在等腰梯形ABCD中,AB=3,CD=1,AE=1,所以DE⊥AB,∴如右图中,DE⊥A1E,DE⊥BE,∴DE⊥面A1EB,故DE⊥A1B,
解:(1)证明:如左图,因为在等腰梯形ABCD中,AB=3,CD=1,AE=1,所以DE⊥AB,∴如右图中,DE⊥A1E,DE⊥BE,∴DE⊥面A1EB,故DE⊥A1B,(2)如图建立空间直角坐标系,设E1A与X轴所的角为θ,则A1(cosθ,-sinθ,0),B(0,2,0),C(0,1,
| 3 |
| 3 |
| n1 |
| n2 |
|
令z=1,则
| n1 |
| ||
| cosθ |
| n1 |
| n2 |
| ||
| 2 |
|
| ||||
|
| ||
| 2 |
此时,点A1在X轴上,A1(1,0,0),
| A1C |
| n1 |
| 3 |
| n3 |
|
| n3 |
| ||
| 3 |
| n1 |
| n3 |
| ||||
|
|
| 7 |
| 8 |
结合图形,可得二面角B-A1C-D为钝角,故二面角的余弦值为-
| 7 |
| 8 |
点评:本题考查二面角的平面角的求法,做题的关键是熟练掌握向量法求二面角的公式与步骤,利用向量法求二面角是向量的一个重要运用,向量的引入,为立体几何中二面角求解带来了极大的方便,题后应注意总结此法求二面角的规律.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
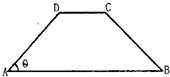 如图,在等腰梯形ABCD中,AB∥CD,且AB=2AD,设∠DAB=θ,θ∈(0,
如图,在等腰梯形ABCD中,AB∥CD,且AB=2AD,设∠DAB=θ,θ∈(0,| π |
| 2 |
| A、随着角度θ的增大,e1增大,e1e2为定值 |
| B、随着角度θ的增大,e1减小,e1e2为定值 |
| C、随着角度θ的增大,e1增大,e1e2也增大 |
| D、随着角度θ的增大,e1减小,e1e2也减小 |
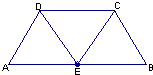 如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点,将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合于点P,则三棱锥P-DCE的外接球的体积为
如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点,将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合于点P,则三棱锥P-DCE的外接球的体积为 在等腰梯形ABCD中,E、F分别是CD、AB中点,CD=2,AB=4,AD=BC=
在等腰梯形ABCD中,E、F分别是CD、AB中点,CD=2,AB=4,AD=BC= 如图,在等腰梯形ABCD中,M,N分别是AB,CD的中点,沿MN将MNCB折起至MNC1B1,使它与MNDA成直二面角.已知AB=2CD=4MN,给出下列四个等式:
如图,在等腰梯形ABCD中,M,N分别是AB,CD的中点,沿MN将MNCB折起至MNC1B1,使它与MNDA成直二面角.已知AB=2CD=4MN,给出下列四个等式: 如图,在等腰梯形ABCD中,AB=6,CD=4,梯形ABCD的面积是
如图,在等腰梯形ABCD中,AB=6,CD=4,梯形ABCD的面积是