题目内容
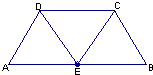如图，在等腰梯形ABCD中，AB=2DC=2，∠DAB=60°，E为AB的中点，将△ADE与△BEC分别沿ED、EC向上折起，使A、B重合于点P，则三棱锥P-DCE的外接球的体积为分析：判定三棱锥的形状，确定外接球的球心位置，找出半径并求解，然后求出球的体积．
解答：解：∵∠DAB=60°∴三棱锥P-DCE各边长度均为1
∴三棱锥P-DCE为正三棱锥 P点在底面DCE的投影为等边△DCE的中心，设中心为O
∴OD=OE=OC=
在直角△POD中：OP2=PD2-OD2=
OP=
∵外接球的球心必在OP上，设球心位置为O'，
则O'P=O'D 设O'P=O'D=R
则在直角△OO'D中：OO'2+OD2=O'D2（OP-O'P）2+OD2=O'D2（
-R）2+（
）2=R2R=
∴体积为
πR3=
故答案为：
∴三棱锥P-DCE为正三棱锥 P点在底面DCE的投影为等边△DCE的中心，设中心为O
∴OD=OE=OC=
| ||
| 3 |
在直角△POD中：OP2=PD2-OD2=
| 2 |
| 3 |
OP=
| ||
| 3 |
∵外接球的球心必在OP上，设球心位置为O'，
则O'P=O'D 设O'P=O'D=R
则在直角△OO'D中：OO'2+OD2=O'D2（OP-O'P）2+OD2=O'D2（
| ||
| 3 |
| ||
| 3 |
| ||
| 4 |
∴体积为
| 4 |
| 3 |
| ||
| 8 |
故答案为：
| ||
| 8 |
点评：本题考查三棱锥的外接球的体积，考查学生空间想象能力，是中档题．
练习册系列答案
相关题目
如图，在等腰梯形ABCD中，AB∥DC，AB=4，CD=2，等腰梯形的高为3，O为AB中点，PO⊥平面ABCD，垂足为O，PO=2，EA∥PO．
如图，在等腰梯形CDEF中，CB、DA是梯形的高，AE=BF=2，AB=2
选修4-1；几何证明选讲．
（2012•河北模拟）如图，在等腰梯形ABCD中，CD=2，AB=4，AD=BC=