题目内容
如图,直线y=kx+2k(k≠0)与x轴交于点B,与双曲线y=(m+5)x2m+1交于点A、C,其中点A在第一象限,点C在第三象限.(1)求双曲线的解析式;
(2)求B点的坐标;
(3)若S△AOB=2,求A点的坐标;
(4)在(3)的条件下,在x轴上是否存在点P,使△AOP是等腰三角形?若存在,请求出P点的坐标;若不存在,请说明理由.

【答案】分析:(1)利用双曲线的定义 (k≠0)即可得出;
(k≠0)即可得出;
(2)由直线y=kx+2k(k≠0),令y=0,解得x即可;
(3)联立 ,解得点A的坐标,再利用2=
,解得点A的坐标,再利用2= ,解得k即可;
,解得k即可;
(4)存在,设P(x,0).分类讨论:①若|OA|=|OP|,②若|AO|=|AP|,③若|PA|=|PO|,再利用两点间的距离公式即可得出.
解答:解:(1)由双曲线y=(m+5)x2m+1,利用双曲线的解析式和图象可得 ,解得m=-1,
,解得m=-1,
∴双曲线的方程为 .
.
(2)由直线y=kx+2k(k≠0),令y=0,解得x=-2,∴B点坐标(-2,0);
(3)联立 ,解得
,解得 ,(∵xA>0),∴
,(∵xA>0),∴ ,
,
∴2= ,即
,即 ,解得k=
,解得k= ,
,
∴xA=2,yA=2,∴A(2,2).
(4)存在,设P(x,0).
①若|OA|=|OP|,则 ,解得x=
,解得x= ;
;
②若|AO|=|AP|,则 ,解得x=4,或x=0(舍去);
,解得x=4,或x=0(舍去);
③若|PA|=|PO|,则 ,解得x=2.
,解得x=2.
综上可知:点P的坐标为以下四个,
( ,(-2
,(-2 ,(2,0),(4,0).
,(2,0),(4,0).
点评:熟练掌握双曲线的定义及其性质、直线与双曲线的相交问题转化为方程联立得到方程组、三角形的面积计算公式、两点间的距离公式、分类讨论的思想方法等是解题的关键.
 (k≠0)即可得出;
(k≠0)即可得出;(2)由直线y=kx+2k(k≠0),令y=0,解得x即可;
(3)联立
 ,解得点A的坐标,再利用2=
,解得点A的坐标,再利用2= ,解得k即可;
,解得k即可;(4)存在,设P(x,0).分类讨论:①若|OA|=|OP|,②若|AO|=|AP|,③若|PA|=|PO|,再利用两点间的距离公式即可得出.
解答:解:(1)由双曲线y=(m+5)x2m+1,利用双曲线的解析式和图象可得
 ,解得m=-1,
,解得m=-1,∴双曲线的方程为
 .
.(2)由直线y=kx+2k(k≠0),令y=0,解得x=-2,∴B点坐标(-2,0);
(3)联立
 ,解得
,解得 ,(∵xA>0),∴
,(∵xA>0),∴ ,
,∴2=
 ,即
,即 ,解得k=
,解得k= ,
,∴xA=2,yA=2,∴A(2,2).
(4)存在,设P(x,0).
①若|OA|=|OP|,则
 ,解得x=
,解得x= ;
;②若|AO|=|AP|,则
 ,解得x=4,或x=0(舍去);
,解得x=4,或x=0(舍去);③若|PA|=|PO|,则
 ,解得x=2.
,解得x=2.综上可知:点P的坐标为以下四个,
(
 ,(-2
,(-2 ,(2,0),(4,0).
,(2,0),(4,0).点评:熟练掌握双曲线的定义及其性质、直线与双曲线的相交问题转化为方程联立得到方程组、三角形的面积计算公式、两点间的距离公式、分类讨论的思想方法等是解题的关键.

练习册系列答案
相关题目
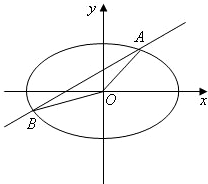 如图,直线y=kx+b与椭圆
如图,直线y=kx+b与椭圆 如图,直线y=kx分抛物线y=x-x2与x轴所围图形为面积相等的两部分,求k的值.
如图,直线y=kx分抛物线y=x-x2与x轴所围图形为面积相等的两部分,求k的值.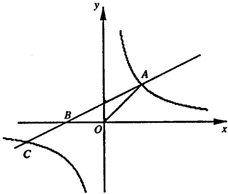 如图,直线y=kx+2k(k≠0)与x轴交于点B,与双曲线y=(m+5)x2m+1交于点A、C,其中点A在第一象限,点C在第三象限.
如图,直线y=kx+2k(k≠0)与x轴交于点B,与双曲线y=(m+5)x2m+1交于点A、C,其中点A在第一象限,点C在第三象限.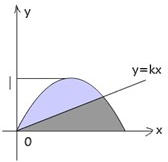 如图,直线
如图,直线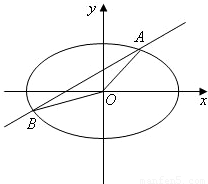 如图,直线y=kx+b与椭圆
如图,直线y=kx+b与椭圆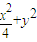 =1交于A,B两点,记△AOB的面积为S.
=1交于A,B两点,记△AOB的面积为S.