题目内容
7.若f(x)=x2-$\sqrt{2}$,则f[f($\sqrt{2}$)]=6-5$\sqrt{2}$.分析 由已知条件利用函数的性质先求出f($\sqrt{2}$)的值,再求f[f($\sqrt{2}$)]的值.
解答 解:∵f(x)=x2-$\sqrt{2}$,
∴$f(\sqrt{2})=(\sqrt{2})^{2}-\sqrt{2}$=2-$\sqrt{2}$,
∴f[f($\sqrt{2}$)]=(2-$\sqrt{2}$)2-$\sqrt{2}$=6-5$\sqrt{2}$.
故答案为:6-5$\sqrt{2}$.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
18.已知实数x,一满足$\left\{\begin{array}{l}{y≥\frac{x}{3}-2}\\{y≤2x+4}\\{2x+3y-12≤0}\end{array}\right.$,直线(2+λ)x-(3+λ)y+(1-2λ)=0(λ∈R)过定点A(x0,y0),则$\frac{y-{y}_{0}}{x-{x}_{0}}$的取值范围为( )
| A. | [$\frac{1}{5}$,7] | B. | [$\frac{1}{7}$,5] | C. | (-∞,$\frac{1}{5}$]∪[7,+∞] | D. | (-∞,$\frac{1}{7}$]∪[5,+∞] |
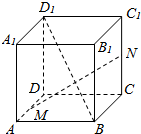 如图所示,在正方体ABCD一A1B1C1D1中,取$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$作为基底.
如图所示,在正方体ABCD一A1B1C1D1中,取$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$作为基底.