Question

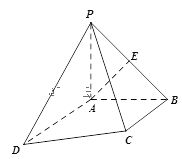
【题目】如图，一块长方形区域，，，在边的中点处有一个可转动的探照灯，其照射角始终为，设，探照灯照射在长方形内部区域的面积为.

（1）求关于的函数关系式；

（2）当时，求的最大值.

Answer 1

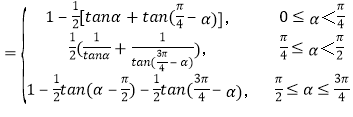【答案】（1）S（2）

【解析】

（1）根据条件讨论α的范围，结合三角形的面积公式进行求解即可．

（2）利用两角和差的三角公式进行化简，结合基本不等式的性质进行转化求解即可．

（1），

则OA＝1，即AE＝tanα，

∠HOFα，

HF＝tan（α），

则△AOE，△HOF得面积分别为tanα，tan（α），

则阴影部分的面积S＝1，，

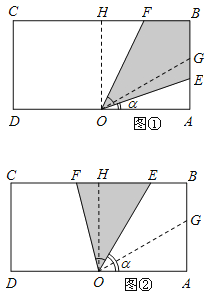
当∈[，）时，E在BH上，F在线段CH上，如图②，

EH，FH，则EF，

则S（），

即，；

同理当，；

即S．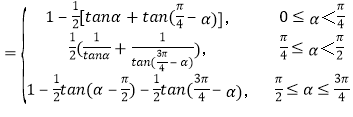

（2）当时，S＝12（1+tanα）

∵0≤tanα≤1，即1≤1+tanα≤2，

则1+tanα22，

当且仅当1+tanα，即1+tanα时取等号，

即，即S的最大值为2