题目内容
已知函数f（x）=tan（2x-bπ）的图象的一个对称中心为（
），若|b|＜
，则f（x）的解析式为
- A.tan（2x+
） - B.tan（2x-
） - C.tan（2x+）或tan（2x-）
- D.tan（2x-）或tan（2x+）
A
分析：根据题中的条件可得tan（
-bπ）=0，故有 （-bπ）=kπ，k∈z，再由|b|＜求得b的值，即得f（x）的解析式．
解答：由题意可得tan（-bπ）=0，∴（-bπ）=kπ，k∈z，∴2-3b=3k，b=
-k，k∈z，
又|b|＜，故b=-
，
故选A．
点评：正切函数的对称性，得到-bπ=kπ，k∈z，是解题的关键．
分析：根据题中的条件可得tan（
-bπ）=0，故有 （-bπ）=kπ，k∈z，再由|b|＜求得b的值，即得f（x）的解析式．解答：由题意可得tan（
-bπ）=0，∴（-bπ）=kπ，k∈z，∴2-3b=3k，b=-k，k∈z，又|b|＜
，故b=-，故选A．
点评：正切函数的对称性，得到
-bπ=kπ，k∈z，是解题的关键． 
练习册系列答案
阅读快车系列答案
相关题目
-1）+lnx，t为常数，且t＞0．
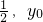）处的切线方程为2x+y-2+ln2，求t和y0的值；
-1）+lnx，t为常数，且t＞0．
）处的切线方程为2x+y-2+ln2，求t和y的值；