题目内容
1．cos240°+tan315°的值为-$\frac{3}{2}$．分析 利用诱导公式化简所给的式子，可得结果．
解答 解：cos240°+tan315°=-cos60°+tan（-45°）=-$\frac{1}{2}$-1=-$\frac{3}{2}$，
故答案为：-$\frac{3}{2}$．
点评 本题主要考查利用诱导公式进行化简求值，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
17．已知某中学高三文科班学生共有800人参加了数学与地理的水平测试，现从中随机抽取100人的数学与地理的水平测试成绩如表：
成绩分为优秀、良好、及格三个等级；横向，纵向分别表示地理成绩与数学成绩，例如：表中数学成绩为良好的共有20+18+4=42
（1）若在该样本中，数学成绩优秀率是30%，求a，b的值；
（2）已知a≥10，b≥8，求数学成绩为优秀的人数比及格的人数少的概率．
| 人数 | 数学 | |||
| 优秀 | 良好 | 及格 | ||
| 地理 | 优秀 | 7 | 20 | 5 |
| 良好 | 9 | 18 | 6 | |
| 及格 | a | 4 | b | |
（1）若在该样本中，数学成绩优秀率是30%，求a，b的值；
（2）已知a≥10，b≥8，求数学成绩为优秀的人数比及格的人数少的概率．
12．设x，y∈R命题p：x＞1且y＞1，q：x+y＞2，则p是q成立的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
9．在等差数列{an}中，a4=5，则a3+a5=（ ）
| A． | 20 | B． | 12 | C． | 10 | D． | 36 |
16．在等比数列{an}中，a1=-16，a4=$\frac{1}{4}$则q=（ ）
| A． | q=$\frac{1}{4}$ | B． | q=-$\frac{1}{4}$ | C． | q=4 | D． | q=-4 |
6．函数f（x）的导函数f'（x），满足关系式f（x）=x2+2xf'（2）-lnx，则f'（2）的值为（ ）
| A． | $-\frac{7}{2}$ | B． | $\frac{7}{2}$ | C． | $-\frac{9}{2}$ | D． | $\frac{9}{2}$ |
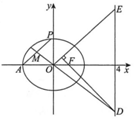如图，已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为为$\frac{1}{2}$，F为椭圆C的右焦点A（-a，0），|AF|=3．