题目内容
解关于x的不等式: <1-a.
<1-a.
解:原不等式化为 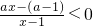 ,
,
即[ax-(a-1)](x-1)<0…(3分)
若a>0,有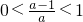 ,原不等式的解集为
,原不等式的解集为 <x<1;
<x<1;
若a=0,有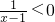 ,原不等式的解集为 x<1;
,原不等式的解集为 x<1;
若a<0,有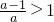 ,原不等式的解集为x<1或
,原不等式的解集为x<1或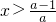 .
.
故(1)若a>0,解集为( ,1)
,1)
(2)若a=0,解集为 (-∞,1)
(3)若a<0,解集为(-∞,1)∪( ,+∞)
,+∞)
分析:通过移项、通分,将不等式化为右边为0的二次不等式,通过对二次不等式对应的二次方程的两个根大小的讨论,据二次不等式解集的形式,写出不等式的解集.
点评:求含参数的分式不等式转化为一元二次不等式的解集问题,属于基础题.解决此类问题一般需要讨论,讨论的起点往往从求知数的系数的正负、判别式的正负两个根的大小进行讨论.
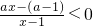 ,
,即[ax-(a-1)](x-1)<0…(3分)
若a>0,有
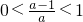 ,原不等式的解集为
,原不等式的解集为 <x<1;
<x<1;若a=0,有
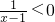 ,原不等式的解集为 x<1;
,原不等式的解集为 x<1;若a<0,有
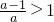 ,原不等式的解集为x<1或
,原不等式的解集为x<1或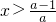 .
. 故(1)若a>0,解集为(
 ,1)
,1)(2)若a=0,解集为 (-∞,1)
(3)若a<0,解集为(-∞,1)∪(
 ,+∞)
,+∞)分析:通过移项、通分,将不等式化为右边为0的二次不等式,通过对二次不等式对应的二次方程的两个根大小的讨论,据二次不等式解集的形式,写出不等式的解集.
点评:求含参数的分式不等式转化为一元二次不等式的解集问题,属于基础题.解决此类问题一般需要讨论,讨论的起点往往从求知数的系数的正负、判别式的正负两个根的大小进行讨论.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目