题目内容
设一汽车在前进途中要经过4个路口,汽车在每个路口遇到绿灯的概率为| 3 |
| 4 |
| 1 |
| 4 |
(Ⅰ)ξ的概率的分布列及期望Eξ;
(Ⅱ)停车时最多已通过3个路口的概率.
分析:(I)由题意知ξ表示停车时已经通过的路口数,因为共有4个路口,ξ的所有可能值为0,1,2,3,4,根据条件所给的在每个路口遇到绿灯的概率为
,遇到红灯(禁止通行)的概率为
,做出变量对应不同数值时的概率,得到分布列和期望.
(II)停车时最多已通过3个路口的对立事件是停车时已经通过4个路口,根据上一问做出的通过4个路口的概率和对立事件的概率,得到结果.
| 3 |
| 4 |
| 1 |
| 4 |
(II)停车时最多已通过3个路口的对立事件是停车时已经通过4个路口,根据上一问做出的通过4个路口的概率和对立事件的概率,得到结果.
解答:解:(I)由题意知ξ的所有可能值为0,1,2,3,4
用AK表示“汽车通过第k个路口时不停(遇绿灯)”,
则P(AK)=
(k=1,2,3,4),且A1,A2,A3,A4独立.
故P(ξ=0)=P(
)=
,
P(ξ=1)=P(A1•
)=
×
=
P(ξ=2)=P(A1•A2•
)=(
)2
=
,
P(ξ=3)=P(A1•A2•A3•
)=(
)3
=
,
P(ξ=4)=P(A1•A2•A3•A4)=(
)4=
从而ζ有分布列:
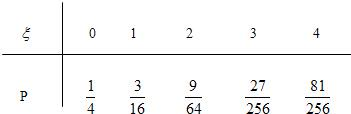
Eξ=0×
+1×
+2×
+3×
+4×
=
(II)P(ξ≤3)=1-P(ξ=4)=1-
=
即停车时最多已通过3个路口的概率为
.
用AK表示“汽车通过第k个路口时不停(遇绿灯)”,
则P(AK)=
| 3 |
| 4 |
故P(ξ=0)=P(
| A1 |
| 1 |
| 4 |
P(ξ=1)=P(A1•
| A2 |
| 3 |
| 4 |
| 1 |
| 4 |
| 3 |
| 16 |
P(ξ=2)=P(A1•A2•
| A3 |
| 3 |
| 4 |
| 1 |
| 4 |
| 9 |
| 64 |
P(ξ=3)=P(A1•A2•A3•
| A4 |
| 3 |
| 4 |
| 1 |
| 4 |
| 27 |
| 256 |
P(ξ=4)=P(A1•A2•A3•A4)=(
| 3 |
| 4 |
| 81 |
| 256 |
从而ζ有分布列:
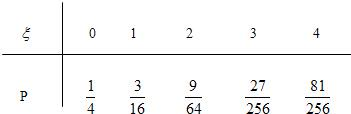
Eξ=0×
| 1 |
| 4 |
| 3 |
| 16 |
| 9 |
| 64 |
| 27 |
| 256 |
| 81 |
| 256 |
| 525 |
| 256 |
(II)P(ξ≤3)=1-P(ξ=4)=1-
| 81 |
| 256 |
| 175 |
| 256 |
即停车时最多已通过3个路口的概率为
| 175 |
| 256 |
点评:本题考查相互独立事件同时发生的概率,对立事件的概率,离散型随机变量的分布列和期望,是一个近几年经常出现的概率问题,解题时注意分清事件的关系.

练习册系列答案
相关题目
 ,遇到红灯(禁止通行)的概率为
,遇到红灯(禁止通行)的概率为 假定汽车只在遇到红灯或到达目的地才停止前进,
假定汽车只在遇到红灯或到达目的地才停止前进, 表示停车时已经通过的路口数,求:
表示停车时已经通过的路口数,求: