题目内容
已知:函数
(1)求函数f(x)的最大值及此时x的值;
(2)在△ABC中,a,b,c分别为内角A,B,C所对的边,且对f(x)定义域中的任意的x都有f(x)≤f(A),若a=2,求 的最大值.
的最大值.
解:(1)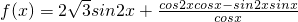 =
=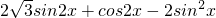 (2分)=
(2分)=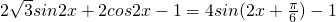 (3分)
(3分)
所以当 时,f(x)取最大值3,
时,f(x)取最大值3,
此时 (5分)
(5分)
(2)由f(A)是f(x)的最大值及A∈(0,π)得到,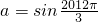 (6分)
(6分)
将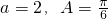 代入b2+c2-a2=2bccosA可得
代入b2+c2-a2=2bccosA可得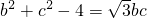 ,
,
又∵b2+c2≥2bc,∴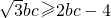 ,∴
,∴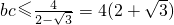 (8分)
(8分)
∴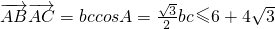
当且仅当b=c时 最大,最大值为
最大,最大值为 (10分)
(10分)
分析:(1)利用两角和与二倍角公式化简函数 为:
为: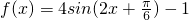 然后求函数f(x)的最大值及此时x的值.
然后求函数f(x)的最大值及此时x的值.
(2)在△ABC中,a,b,c分别为内角A,B,C所对的边,且对f(x)定义域中的任意的x都有f(x)≤f(A),推出f(A)是f(x)的最大值及A∈(0,π),求出A,通过余弦定理,和基本不等式确定bc的范围,然后求出 的表达式,即可求出它的最大值.
的表达式,即可求出它的最大值.
点评:本题考查三角函数的最值,平面向量数量积的坐标表示,基本不等式的应用,二倍角和两角和的正弦函数的应用是解题的关键,(2)是有难度的小综合题目,挖掘f(A)是f(x)的最大值,比较重要,灵活应用不等式求最值.
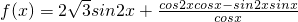 =
=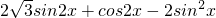 (2分)=
(2分)=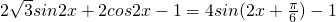 (3分)
(3分)所以当
 时,f(x)取最大值3,
时,f(x)取最大值3,此时
 (5分)
(5分)(2)由f(A)是f(x)的最大值及A∈(0,π)得到,
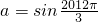 (6分)
(6分)将
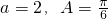 代入b2+c2-a2=2bccosA可得
代入b2+c2-a2=2bccosA可得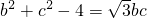 ,
,又∵b2+c2≥2bc,∴
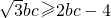 ,∴
,∴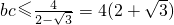 (8分)
(8分)∴
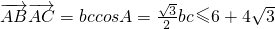
当且仅当b=c时
 最大,最大值为
最大,最大值为 (10分)
(10分)分析:(1)利用两角和与二倍角公式化简函数
 为:
为: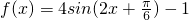 然后求函数f(x)的最大值及此时x的值.
然后求函数f(x)的最大值及此时x的值.(2)在△ABC中,a,b,c分别为内角A,B,C所对的边,且对f(x)定义域中的任意的x都有f(x)≤f(A),推出f(A)是f(x)的最大值及A∈(0,π),求出A,通过余弦定理,和基本不等式确定bc的范围,然后求出
 的表达式,即可求出它的最大值.
的表达式,即可求出它的最大值.点评:本题考查三角函数的最值,平面向量数量积的坐标表示,基本不等式的应用,二倍角和两角和的正弦函数的应用是解题的关键,(2)是有难度的小综合题目,挖掘f(A)是f(x)的最大值,比较重要,灵活应用不等式求最值.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目