题目内容
已知向量
=(1,-3,2),
=(-2,1,1),点A(-3,-1,4),B(-2,-2,2).
(1)求:|2
+
|;
(2)在直线AB上,是否存在一点E,使得
⊥
?(O为原点)
| a |
| b |
(1)求:|2
| a |
| b |
(2)在直线AB上,是否存在一点E,使得
| OE |
| b |
(1)2
+
=(2,-6,4)+(-2,1,1)=(0,-5,5),
∴|2
+
|=
=5
;
(2)假设存在点E(x,y,z)满足条件,
则
∥
,且得
•
=0,
又
=(x+3,y+1,z-4),
=(1,-1,-2),
∴
,解得
,
∴在直线AB上,存在一点E(-3,-1,4),使得
⊥
| a |
| b |
∴|2
| a |
| b |
| 02+(-5)2+52 |
| 2 |
(2)假设存在点E(x,y,z)满足条件,
则
| AE |
| AB |
| OE |
| b |
又
| AE |
| AB |
∴
|
|
∴在直线AB上,存在一点E(-3,-1,4),使得
| OE |
| b |

练习册系列答案
相关题目
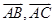 为边的平行四边形的面积为________.
为边的平行四边形的面积为________.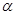 、
、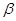 的法向量分别为
的法向量分别为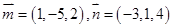 ,则 ( )
,则 ( )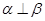
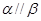
 ,若
,若 ,则
,则 ______。
______。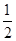 ,y=-
,y=-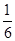 ,y=-
,y=-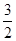
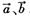 不共线,若
不共线,若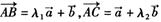 ,且A、B、C三点共线,则关于实数
,且A、B、C三点共线,则关于实数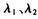 一定成立的关系式为( )
一定成立的关系式为( ) ="1" B.
="1" B.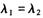 =" -1" C.
=" -1" C.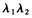 ="1" D.
="1" D.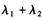 =1
=1