题目内容
设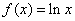 ,
,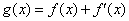 .
.
求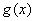 的单调区间和最小值;
的单调区间和最小值;
讨论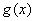 与
与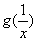 的大小关系;
的大小关系;
(3)求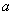 的取值范围,使得
的取值范围,使得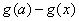 <
<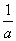 对任意
对任意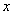 >0成立.
>0成立.
【解】(1)由题设知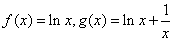 ,∴
,∴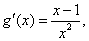 令
令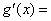 0得
0得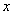 =1,
=1,
当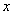 ∈(0,1)时,
∈(0,1)时,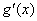 <0,
<0,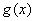 是减函数,故(0,1)是
是减函数,故(0,1)是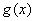 的单调减区间。
的单调减区间。
当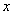 ∈(1,+∞)时,
∈(1,+∞)时,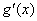 >0,
>0,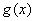 是增函数,故(1,+∞)是
是增函数,故(1,+∞)是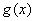 的单调递增区间,
的单调递增区间,
因此,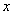 =1是
=1是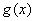 的唯一极值点,且为极小值点,从而是最小值点,所以
的唯一极值点,且为极小值点,从而是最小值点,所以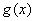 的最小值为
的最小值为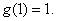
(2)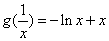 ,设
,设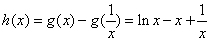 ,则
,则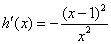 ,
,
当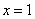 时,
时,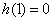 ,即
,即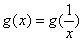 ,当
,当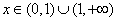 时,
时,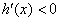 ,
,
因此,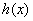 在
在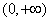 内单调递减,当
内单调递减,当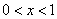 时,
时,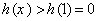 ,即
,即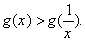
当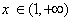 时,
时,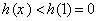 ,
,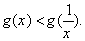 当x=1时,
当x=1时,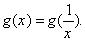
(3)由(1)知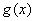 的最小值为1,所以,
的最小值为1,所以,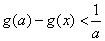 ,对任意
,对任意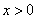 ,成立
,成立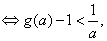
即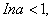 从而得
从而得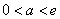 。
。

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
设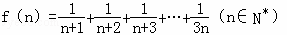 ,则f(n+1)﹣f(n)=( )
,则f(n+1)﹣f(n)=( )
|
| A. |
| B. |
|
|
| C. |
| D. |
|
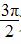 )(x∈R),下面结论错误的是( )
)(x∈R),下面结论错误的是( )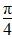 对称
对称 ]上是增函数
]上是增函数 -α)=
-α)= ,α∈(0,
,α∈(0, =________.
=________.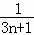

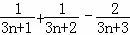
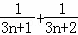
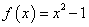 .对任意
.对任意 ,
,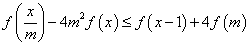
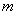 的取值范围是 .
的取值范围是 .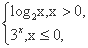 且函数F(x)=f(x)+x-a有且仅有两个零点,则实数a的取值范围是 .
且函数F(x)=f(x)+x-a有且仅有两个零点,则实数a的取值范围是 .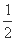 ax2+2x,g(x)=ln x.
ax2+2x,g(x)=ln x.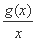 =f'(x)-(2a+1)在区间
=f'(x)-(2a+1)在区间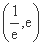 内有且只有两个不相等的实数根?若存在,请求出a的取值范围;若不存在,请说明理由.
内有且只有两个不相等的实数根?若存在,请求出a的取值范围;若不存在,请说明理由.