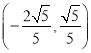Question

【题目】已知函数，若在定义域内存在，使得成立，则称为函数的“局部对称点”.

（1），其中，试判断是否有“局部对称点”？若有，请求出该点；若没有，请说明理由；

（2）若函数在区间内有“局部对称点”，求实数m的取值范围；

（3）若函数在R上有“局部对称点”，求实数m的取值范围.

Answer 1

【答案】（1）有，理由见解析；（2）；（3）.

【解析】

（1）根据“局部对称点”的概念，列出方程，求解函数的 “局部对称点”；

（2）根据题意，则列方程，使方程有解，运用换元法，设，则，求解的范围，即可求解的范围.

（3）根据题意，列出方程，并且转化方程为，运用换元法，令，则，转化为关于的一元二次方程，在区间内有解的问题，限定条件，即可求解.

（1）知

由于，故，

当时有，即为“局部对称点”.

（2）方程在区间上有解，于是

设（），，则，其中

所以

（3），

由于，所以

于是（*）在R上有解；

令（），则，所以方程（*）变为在区间内有解；

设，可分为以下两种情形：

当时，有，化简得

解得；

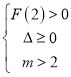②当时，有，化简得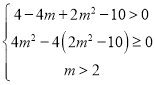

解得

综上所述，