题目内容
已知双曲线顶点间的距离为6,一条渐近线方程为y=
,求双曲线的标准方程.
| 3x | 2 |
分析:根据双曲线的一条渐近线方程为y=
,设出双曲线方程,结合两顶点之间的距离为6,从而可求双曲线的标准方程.
| 3x |
| 2 |
解答:解:当焦点在x轴上时,设双曲线的方程为:
x2-y2=k(k>0)
∵两顶点之间的距离为6,
∴2
=6,∴k=
,
∴双曲线的方程为
-
=1;
当双曲线的焦点在y轴上
设双曲线的方程为:y2-
x2=k(k>0)
两顶点之间的距离为6,
∴2
=6,∴k=9,
∴双曲线的方程为
-
=1.
∴双曲线的方程为
-
=1或
-
=1.
| 9 |
| 4 |
∵两顶点之间的距离为6,
∴2
|
| 81 |
| 4 |
∴双曲线的方程为
| x2 |
| 9 |
| y2 | ||
|
当双曲线的焦点在y轴上
设双曲线的方程为:y2-
| 9 |
| 4 |
两顶点之间的距离为6,
∴2
|
∴双曲线的方程为
| y2 |
| 9 |
| x2 |
| 4 |
∴双曲线的方程为
| x2 |
| 9 |
| y2 | ||
|
| y2 |
| 9 |
| x2 |
| 4 |
点评:本题以双曲线的性质为载体,考查双曲线的标准方程,解题的关键是确定双曲线的焦点在x轴上还是在y轴上.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 ,点
,点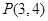 在椭圆上,求它的方程 (2)已知双曲线顶点间的距离为6,渐近线方程为
在椭圆上,求它的方程 (2)已知双曲线顶点间的距离为6,渐近线方程为 ,求它的方程.
,求它的方程. x,求它的方程.
x,求它的方程. x,求它的方程。
x,求它的方程。