Question

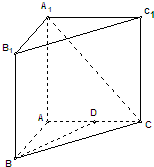（2012•浦东新区一模）如图，直三棱柱ABC-A₁B₁C₁中，AB=AC=AA₁=2，∠ABC=45°．
（1）求直三棱柱ABC-A₁B₁C₁的体积；
（2）若D是AC的中点，求异面直线BD与A₁C所成的角．

Answer 1

分析：（1）利用三棱柱的体积计算公式即可得出；
（2）利用三角形的中位线定理和异面直线所成的角的定义即可得出．

解答：解：（1）∵AB=AC=2，∠ABC=45°，∴∠BAC=90°，∴S△ABC=

1

2

×2×2=2．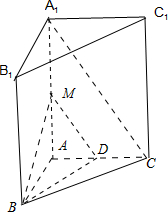
又AA₁=2，∴直三棱柱ABC-A₁B₁C₁的体积V=S_△ABC×AA₁=2×2=4．
∴直三棱柱ABC-A₁B₁C₁的体积为4．
（2）取AA₁的中点M，连接DM，BM，
∵D是AC的中点，∴DM∥A₁C，
∴∠BDM是异面直线BD与A₁C所成的角．
在△BDM中，BD=BM=

5

，MD=

2

，cos∠BDM=

( 5 )2+( 2 )2-( 5 )2

2• 2 • 5

=

10

10

．即∠BDM=arccos

10

10

．
∴异面直线BD与A₁C所成的角为arccos

10

10

．

点评：熟练掌握三棱柱的体积计算公式、三角形的中位线定理和异面直线所成的角的定义是解题的关键．