题目内容
(14分)已知函数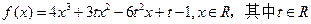 ,
,
(1)当t=1时,求曲线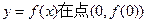 处的切线方程;
处的切线方程;
(2)当t≠0时,求的单调区间;
(3)证明:对任意的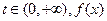 在区间(0,1)内均存在零点。
在区间(0,1)内均存在零点。
(1)当t=1时, 解析 已知函数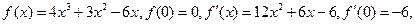
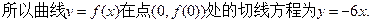
(2)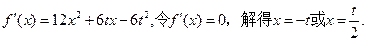

因为t≠0,以下分两种情况讨论:
①若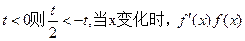 的变化情况如下表:
的变化情况如下表:
所以,x 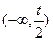
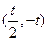
(-t,∞) 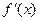
+ - + 



 的单调递增区间是
的单调递增区间是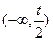 ,(-t,∞)
,(-t,∞) ;
; 的单调递减区间是
的单调递减区间是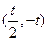 。
。
②若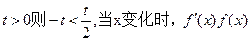 的变化情况如下表:
的变化情况如下表:x (-∞,t) 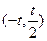
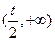
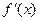
+  练习册系列答案
练习册系列答案
1加1阅读好卷系列答案
专项复习训练系列答案
初中语文教与学阅读系列答案

完形填空与阅读理解周秘计划系列答案
英语阅读理解150篇系列答案
奔腾英语系列答案
标准阅读系列答案
53English系列答案
考纲强化阅读系列答案
相关题目
 ,则
,则 ( )
( )A. 
B. 
C. 
D. 
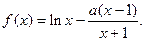 (
(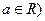
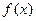 在定义域上为单调增函数,求
在定义域上为单调增函数,求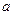 的取值范围;
的取值范围;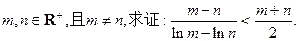
 .
.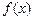 为定义域上的单调函数,求实数m的取值范围;
为定义域上的单调函数,求实数m的取值范围;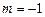 时,求函数
时,求函数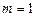 ,且
,且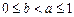 时,证明:
时,证明: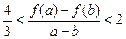 .
.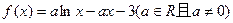 .
. 的单调区间;
的单调区间;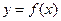 的图像在点
的图像在点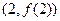 处的切线的倾斜角为
处的切线的倾斜角为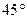 ,问:
,问: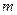 在什么范围取值时,对于任意的
在什么范围取值时,对于任意的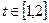 ,函数
,函数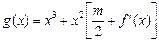 在区间
在区间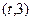 上总存在极值?
上总存在极值?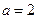 时,设函数
时,设函数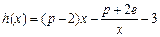 ,若在区间
,若在区间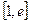 上至少存在
上至少存在 一个
一个 ,
,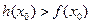 成立,试求实数
成立,试求实数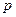 的取值范围.
的取值范围.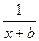 (a,b∈Z),曲线y=f(x)在点(2,f(2))处的切线方
(a,b∈Z),曲线y=f(x)在点(2,f(2))处的切线方 是定义在
是定义在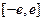 上的奇函数,当
上的奇函数,当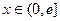 时,
时,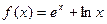 ,其中
,其中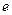 是自然对数的底数.
是自然对数的底数.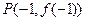 处的切线方程.
处的切线方程.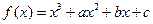 在
在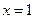 与
与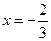 时,都取得极值。
时,都取得极值。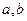 的值;
的值;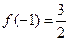 ,求
,求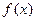 的单调区间和极值;
的单调区间和极值;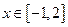 都有
都有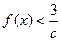 恒成立,求
恒成立,求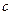 的取值范围。
的取值范围。