题目内容
若sinθ,cosθ是方程4x2+2mx+m=0的两根,则sinθ+cosθ的值为
- A.

- B.

- C.

- D.

B
分析:由判别式△大于或等于零求得 m≤0,或 m≥4,再由一元二次方程的根与系数的关系可得 sinθ+cosθ=- ,sinθ•cosθ=
,sinθ•cosθ= .再由sin2θ+cos2θ=1,可得
.再由sin2θ+cos2θ=1,可得 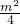 =
= +1,由此求得m的值,进而求得sinθ+cosθ的值.
+1,由此求得m的值,进而求得sinθ+cosθ的值.
解答:∵sinθ,cosθ是方程4x2+2mx+m=0的两根,则判别式△=4m2-16m≥0,解得 m≤0,或 m≥4.
再由根与系数的关系可得 sinθ+cosθ=- ,sinθ•cosθ=
,sinθ•cosθ= .
.
再由同角三角函数的基本关系sin2θ+cos2θ=1可得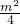 =
= +1,解得m=
+1,解得m= +1(舍去),或 m=1-
+1(舍去),或 m=1- .
.
∴sinθ+cosθ=- =-
=- =
= .
.
故选B.
点评:本题主要考查一元二次方程的根与系数的关系,同角三角函数的基本关系的应用,属于基础题.
分析:由判别式△大于或等于零求得 m≤0,或 m≥4,再由一元二次方程的根与系数的关系可得 sinθ+cosθ=-
 ,sinθ•cosθ=
,sinθ•cosθ= .再由sin2θ+cos2θ=1,可得
.再由sin2θ+cos2θ=1,可得 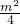 =
= +1,由此求得m的值,进而求得sinθ+cosθ的值.
+1,由此求得m的值,进而求得sinθ+cosθ的值.解答:∵sinθ,cosθ是方程4x2+2mx+m=0的两根,则判别式△=4m2-16m≥0,解得 m≤0,或 m≥4.
再由根与系数的关系可得 sinθ+cosθ=-
 ,sinθ•cosθ=
,sinθ•cosθ= .
.再由同角三角函数的基本关系sin2θ+cos2θ=1可得
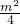 =
= +1,解得m=
+1,解得m= +1(舍去),或 m=1-
+1(舍去),或 m=1- .
.∴sinθ+cosθ=-
 =-
=- =
= .
.故选B.
点评:本题主要考查一元二次方程的根与系数的关系,同角三角函数的基本关系的应用,属于基础题.

练习册系列答案
相关题目
若sin(
+α)+cos(α-
)=
,则sin(
+α)+cos(α-
)=( )
| π |
| 2 |
| π |
| 2 |
| 7 |
| 5 |
| 3π |
| 2 |
| 3π |
| 2 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|