题目内容
平面上给定一个锐角三角形ABC，过顶点B的高交以AC为直径的圆于P、Q,过顶点C的高交以AB为直径的圆于M、N，求证：M，N，P，Q四点共圆.证明：设以AB、AC为直径的两圆的另一交点为D（如图），
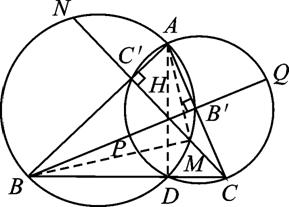
则∠ADC=∠ADB=90°，故AD为BC边上的高，且AD过BB′与CC′的交点H,
由N、A、M、D共圆有NH·HM=AH·HD，由P、A、Q、D共圆有PH·HQ=AH·HD，所以NH·HM=PH·HQ，故M、N、P、Q四点共圆.
练习册系列答案
相关题目
的所有解；
所表示的平面区域是一个锐角三角形，则a的取值范围是
．