题目内容
(2013•房山区一模)若不等式组
表示的平面区域是一个锐角三角形,则k的取值范围是
|
(-1,0)
(-1,0)
.分析:作出题中不等式组表示的平面区域,得如图的△ABC及其内部,再将直线AC:y=kx+5绕A点旋转并观察△ABC形状的变化,可得当点C位于C1、C2之间时,△ABC是锐角三角形,由此建立关于k的不等式组,解之即可得到k的取值范围.
解答:解: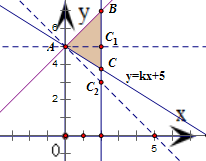 作出不等式组
作出不等式组
表示的平面区域,
得到如图的△ABC及其内部,其中A(0,5),B(2,7),C(2,2k+5)
△ABC的形状随着直线AC:y=kx+5斜率的变化而变化,
将直线AC绕A点旋转,可得
当C点与C1(2,5)重合或与C2(2,3)重合时,△ABC是直角三角形,
当点C位于B、C1之间,或在C1C2的延长线上时,△ABC是钝角三角形,
当点C位于C1、C2之间时,△ABC是锐角三角形,
而点C在其它的位置不能构成三角形
综上所述,可得3<2k+5<5,解之得-1<k<0
即k的取值范围是(-1,0)
故答案为:(-1,0)
 作出不等式组
作出不等式组
|
得到如图的△ABC及其内部,其中A(0,5),B(2,7),C(2,2k+5)
△ABC的形状随着直线AC:y=kx+5斜率的变化而变化,
将直线AC绕A点旋转,可得
当C点与C1(2,5)重合或与C2(2,3)重合时,△ABC是直角三角形,
当点C位于B、C1之间,或在C1C2的延长线上时,△ABC是钝角三角形,
当点C位于C1、C2之间时,△ABC是锐角三角形,
而点C在其它的位置不能构成三角形
综上所述,可得3<2k+5<5,解之得-1<k<0
即k的取值范围是(-1,0)
故答案为:(-1,0)
点评:本题给出二元一次不等式组,在表示的图形为锐角三角形的情况下,求参数k的取值范围,着重考查了二元一次不等式组表示的平面区域和简单的线性规划等知识,属于基础题.

练习册系列答案
相关题目
 (2013•房山区一模)执行如图所示的程序框图.若输出S=15,则框图中①处可以填入( )
(2013•房山区一模)执行如图所示的程序框图.若输出S=15,则框图中①处可以填入( ) (2013•房山区一模)在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,ABCD为直角梯形,BC∥AD,∠ADC=90°,
(2013•房山区一模)在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,ABCD为直角梯形,BC∥AD,∠ADC=90°,