题目内容
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() ,以
,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 在曲线
在曲线![]() 上,直线
上,直线![]() 交曲线
交曲线![]() 于点
于点![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ;(2)
;(2)![]() .
.
【解析】
(1)由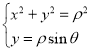 可将曲线
可将曲线![]() 的方程化为极坐标方程,在曲线
的方程化为极坐标方程,在曲线![]() 的极坐标方程两边平方得
的极坐标方程两边平方得![]() ,由
,由![]() 可将曲线
可将曲线![]() 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)根据题意得出![]() ,
,![]() ,然后利用换元法和三角函数关系式的恒等变换并结合基本不等式可求出
,然后利用换元法和三角函数关系式的恒等变换并结合基本不等式可求出![]() 的最小值.
的最小值.
(1)将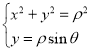 代入
代入![]() 得,
得,![]() ,
,
所以曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
曲线![]() 的方程可化为
的方程可化为![]() ,
,
即![]() ,得
,得![]() ,
,
所以![]() 的直角坐标方程为
的直角坐标方程为![]() ;
;
(2)由(1)及题设条件知,![]() ,
,![]() ,其中
,其中![]() ,
,
所以![]() ,令
,令![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以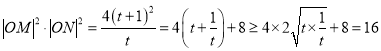 ,
,
当且仅当![]() ,即
,即![]() ,
,![]() 时等号成立.
时等号成立.
所以![]() 的最小值为
的最小值为![]() .
.

 口算题天天练系列答案
口算题天天练系列答案【题目】甲、乙两个商场同时出售一款西门子冰箱,其中甲商场位于老城区中心,乙商场位于高新区.为了调查购买者的年龄与购买冰箱的商场选择是否具有相关性,研究人员随机抽取了1000名购买此款冰箱的用户作调研,所得结果如表所示:
50岁以上 | 50岁以下 | |
选择甲商场 | 400 | 250 |
选择乙商场 | 100 | 250 |
(1)判断是否有![]() 的把握认为购买者的年龄与购买冰箱的商场选择具有相关性;
的把握认为购买者的年龄与购买冰箱的商场选择具有相关性;
(2)由于乙商场的销售情况未达到预期标准,商场决定给冰箱的购买者开展返利活动具体方案如下:当天卖出的前60台(含60台)冰箱,每台商家返利200元,卖出60台以上,超出60台的部分,每台返利50元.现将返利活动开展后15天内商场冰箱的销售情况统计如图所示:与此同时,老张得知甲商场也在开展返利活动,其日返利额的平均值为11000元,若老张将选择返利较高的商场购买冰箱,请问老张应当去哪个商场购买冰箱

附: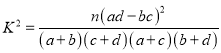 ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |