题目内容
【题目】已知函数f(x)=ax2+x﹣lnx,(a>0). (Ⅰ)求f(x)的单调区间;
(Ⅱ)设f(x)极值点为x0 , 若存在x1 , x2∈(0,+∞),且x1≠x2 , 使f(x1)=f(x2),求证:x1+x2>2x0 .
【答案】解:( I)f(x)定义域为(0,+∞), f′(x)= ![]() ,
,
∵a>0,∴方程f′(x)=0有两个实根x1= ![]() <0,x2=
<0,x2= ![]() >0,
>0,
当x∈(0,x2)时,f′(x)<0,当x∈(x2 , +∞)时,f′(x)>0,
∴f(x)的单调增区间为:( ![]() ,+∞)减区间为(0,
,+∞)减区间为(0, ![]() )
)
( II)要证x1+x2>2x0 , 需证 ![]() .
.
由( I)知, ![]() ,f′(x)=2ax+1﹣
,f′(x)=2ax+1﹣ ![]() 在(0,+∞)上单调递增,
在(0,+∞)上单调递增,
∴只需证f′( ![]() )>0
)>0
不妨设x2>x1>0
由已知得 ![]() =
= ![]() ,=[a(x2+x1)+1](x2﹣x1)﹣(lnx2﹣lnx1)=0
,=[a(x2+x1)+1](x2﹣x1)﹣(lnx2﹣lnx1)=0
∴ ![]()
∵ ![]()
∴ ![]()
法1: ![]() =
= ![]()
令 ![]()
∴ 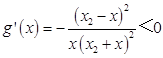 ,∴g(x)在(0,x2)单调递减,
,∴g(x)在(0,x2)单调递减,
∴g(x1)>g(x2)=0,
又 ![]() ,∴
,∴ ![]() 成立.∴结论成立.
成立.∴结论成立.
法2:f′( ![]() )=
)= 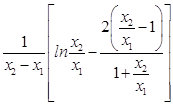 .
.
设 ![]() ,
, ![]() .∵
.∵ 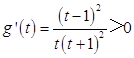 ,
,
∴g(t)在(1,+∞)上是增函数,∴g(t)>g(1)=0,
即 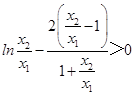 ,
,
又∵ ![]() ,∴f′(
,∴f′( ![]() )>0成立.
)>0成立.
∴结论成立
【解析】(Ⅰ)先求出函数的定义域,求出函数f(x)的导函数,在定义域下令导函数大于0得到函数的递增区间.即可求出单调减区间.(Ⅱ)要证x1+x2>2x0 , 需证 ![]() .由( I)知,
.由( I)知, ![]() ,f′(x)=2ax+1﹣
,f′(x)=2ax+1﹣ ![]() 在(0,+∞)上单调递增,只需证f′(
在(0,+∞)上单调递增,只需证f′( ![]() )>0.
)>0.
【考点精析】掌握利用导数研究函数的单调性和函数的极值与导数是解答本题的根本,需要知道一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.

 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案【题目】为了政府对过热的房地产市场进行调控决策,统计部门对城市人和农村人进行了买房心理预测调研,用简单随机抽样的方法抽取了110人进行统计,得到如下列联表:
买房 | 不买房 | 纠结 | |
城市人 | 5 | 15 | |
农村人 | 20 | 10 |
已知样本中城市人数与农村人数之比是3:8.
(Ⅰ)分别求样本中城市人中的不买房人数和农村人中的纠结人数;
(Ⅱ)从参与调研的城市人中用分层抽样方法抽取6人,进一步统计城市人的某项收入指标,假设一个买房人的指标算作3,一个纠结人的指标算作2,一个不买房人的指标算作1,现在从这6人中再随机选取3人,令X=再抽取3人指标之和,求X的分布列和数学期望.