题目内容
17.设数列{an}前n项和为Sn,已知Sn=2an-1(n∈N*),(1)求数列{an}的通项公式;
(2)若对任意的n∈N*,不等式k(Sn+1)≥2n-9恒成立,求实数k的取值范围.
分析 (1)求出数列的首项,利用an=Sn-Sn-1,求解数列的通项公式.
(2)由k(Sn+1)≥2n-9,整理得k≥$\frac{2n-9}{2^n}$,令${b_n}=\frac{2n-9}{2^n}$,判断数列的单调性,求出最大项,然后求解实数k的取值范围.
解答 解:(1)令n=1,S1=2a1-1=a1,解得a1=1.…(2分)
由Sn=2an-1,有Sn-1=2an-1-1,
两式相减得an=2an-2an-1,
化简得an=2an-1(n≥2),
∴数列{an}是以首项为1,公比为2 的等比数列,
∴数列{an}的通项公式${a_n}={2^{n-1}}$.…(6分)
(2)由k(Sn+1)≥2n-9,整理得k≥$\frac{2n-9}{2^n}$,
令${b_n}=\frac{2n-9}{2^n}$,则${b_{n+1}}-{b_n}=\frac{2n-7}{{{2^{n+1}}}}-\frac{2n-9}{2^n}=\frac{11-2n}{{{2^{n+1}}}}$,…(8分)
n=1,2,3,4,5时,${b_{n+1}}-{b_n}=\frac{11-2n}{{{2^{n+1}}}}>0$,
∴b1<b2<b3<b4<b5.…(10分)
n=6,7,8,…时,${b_{n+1}}-{b_n}=\frac{11-2n}{{{2^{n+1}}}}<0$,即b6>b7>b8>…
∵b5=$\frac{1}{32}$<${b_6}=\frac{3}{64}$,
∴bn的最大值是${b_6}=\frac{3}{64}$.
∴实数k的取值范围是$[\frac{3}{64},\;\;+∞)$.…(12分)
点评 本题考查数列的递推关系式以及数列与函数相结合,考查构造法以及函数的单调性的应用,考查计算能力.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案| 喜欢冷冻 | 不喜欢冷冻 | 合计 | |
| 女学生 | 60 | 20 | 80 |
| 男学生 | 10 | 10 | 20 |
| 合计 | 70 | 30 | 100 |
(2)已知在被调查的北方学生中有5名高二(15)班的学生,其中2名不喜欢冷冻降暑食品.现在从这5名学生中随机抽取2人,求至多有1人喜欢冷冻降暑食品的概率.
| P(χ2≥k) | 0.100 | 0.050 | 0.010 |
| k | 2.706 | 3.841 | 6.635 |
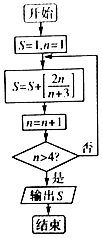 若[x]表示不超过x的最大整数,如[2,6]=2,[-2,6]=-3,执行如图所示的程序框图,记输出的值为S0,则${log_{\frac{1}{3}}}{S_0}$=( )
若[x]表示不超过x的最大整数,如[2,6]=2,[-2,6]=-3,执行如图所示的程序框图,记输出的值为S0,则${log_{\frac{1}{3}}}{S_0}$=( )| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
| A. | a∈(-∞,$\frac{1}{6}$) | B. | a∈(-$\frac{1}{2}$,+∞) | C. | a∈(-$\frac{1}{2}$,$\frac{1}{6}$) | D. | a∈($\frac{1}{2}$,+∞) |